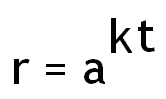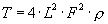Artigos do Prof. Luiz da Silva Netto Ao compartilharmos este material, desejamos prestar um tributo a este eminente professor que, infelizmente, faleceu dia 10 de agosto de 2010. A Compensação da Sobretensão nas Cordas de Instrumentos Musicais A Escala Musical Temperada e os Juros Compostos A Matemática e os Dedos do Instrumentista A Música e os Logaritmos A Razão Áurea e a Geometria da Flor de Cera – Hoya Carnosa A Variação na Simbologia das Claves Musicais ao Longo do Tempo e o Modelo Holográfico Características do Som – A Transformada de Fourier Como Plotar o Valor de uma Nota […]
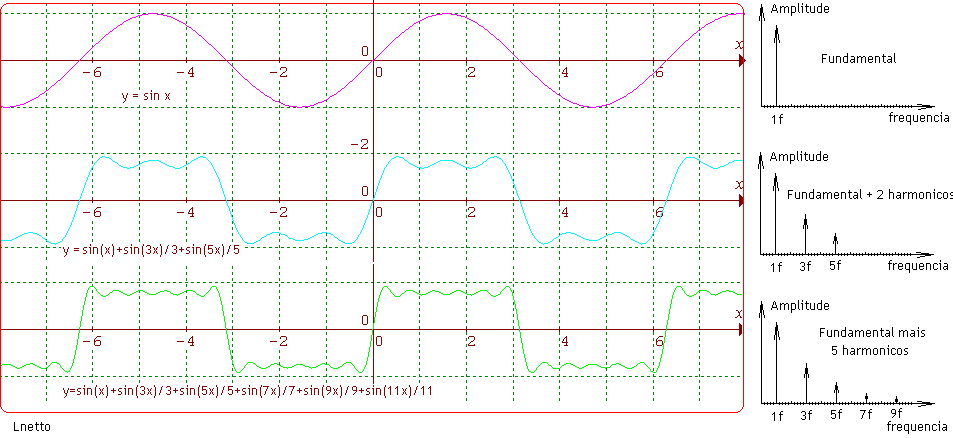
por: Prof.Luiz Netto Prosseguindo em minhas pesquisas para conhecer melhor os instrumentos, resolvi levantar quais os sons harmônicos que aparecem em um acordeão. Embora eu não seja um luthier e tão pouco um instrumentista, tenho instrumentos tais como um acordeão Scandalli, 120 baixos,violino, bandolim, violão, gaita de boca cromática e um pequeno órgão eletrônico. Utilizei para este levantamento o microfone utilizado para gravar mensagens no computador, e um programa analisador de espectro e o resultado poderá ser visto através dos gráficos a seguir. Como poderá ser verificado, aparecem os harmônicos de ordem par e ordem ímpar em relação à frequencia […]
Em relação ao violino, a viola é um pouco maior, com alcance mais grave. Considerando o violino o soprano das cordas, a viola é o contralto, o cello o tenor – barítono e finalmente, o contrabaixo os baixos.
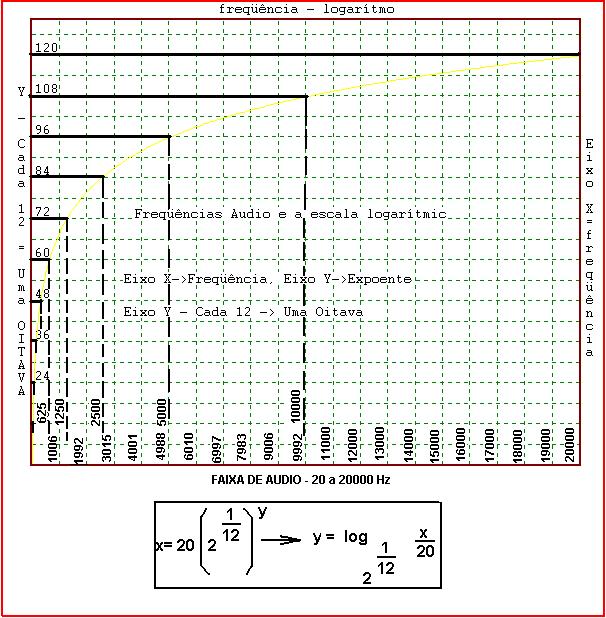
por: Prof.Luiz Netto Faixa de Audio – 20-20000 Hertz Aproximadamente 10 oitavas Frequências de 20 a 1309 Hertz O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil Retornar ao Índice
por: Prof.Luiz Netto São tres os parâmetros que definem um Som: A sua altura, ou seja a frequência, ou número de vibrações produzidas por segundo, a sua intensidade, ou o quanto forte ou quanto potente é o som, e o timbre, caracteristica esta que dá identidade a um instrumento, ou seja sabemos qual instrumento está emitindo um som. Quando vamos assistir a um concerto musical, podemos observar nos momentos que antecede a apresentação musical, os músicos afinando seus instrumentos; tomando por base a nota la3 = 440 Hz, ou ciclos por segundo – e se um violino e um piano […]
por: Prof.Luiz Netto Deus… a natureza…utiliza a Geometria – Uma das Manifestações do número de ouro, relação áurea, segmento áureo ou proporção divina aplicadas nesta flôr. Um dia destes fazendo uma viagem para Araraquara deparei-me na casa de um amigo com esta flor que assombrou-me pela sua beleza geométrica. Tirei algumas fotos e aproveitei já fotos tiradas pelo amigo Sebastião Vicentini Neto. De imediato ocorreu-me relembrar as propriedades da figura geométrica do pentágono regular, que ora faço aqui. Minhas fotos A forma pentagonal regular da Hoya Carnosa Fotos do amigo Sebastião Vicentini Neto – Um dos estágios da evolução da […]
por: Prof.Luiz Netto r = a^(kt) Além da representação da escala musical temperada com seus vetores frequencia representados no espaço bidimensional, podemos fazer esta representação também no espaço tridimensional. Devo dizer que nunca vi isto deste modo, apenas proponho esta maneira de representá-la, como o fiz na representação polar em duas dimensões. Podemos imaginar os vetores girando em torno de um cilindro cujo raio da base tem o valor (1.0594631)^(1.9098593 t) para t = zero, com origens no centro do cilindro e cujas pontas percorram as paredes do cilindro subindo exponencialmente, de acordo com a equação (1.0594631)^(1.9098593 t). A equação […]
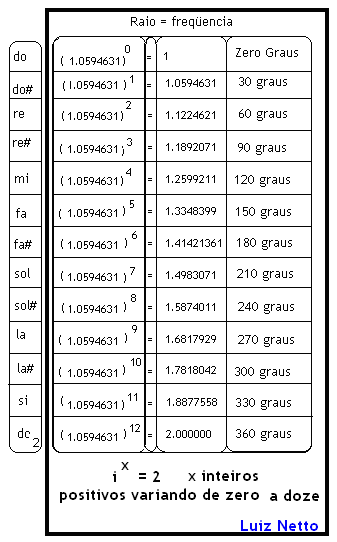
por: Prof.Luiz Netto Intervalos Musicais – O Número 1,0594631 A escala musical temperada pode ser definida matemáticamente como uma progressão geométrica cujo primeiro termo é a frequencia da nota escolhida (Número de oscilações por segundo) e cuja razão é o valor númerico 1.0594631 em decorrencia da divisão de uma oitava em 12 intervalos. (veja a dedução logo mais abaixo). Assim, se tomarmos a nota dó como 16,352 Hz (Hertz) e formos multiplicando sucessivamente pelo número 1.0594631 vamos obter todas as frequencias das notas musicais da escala musical temperada, culminando com a primeira nota da oitava seguinte que é o dobro […]
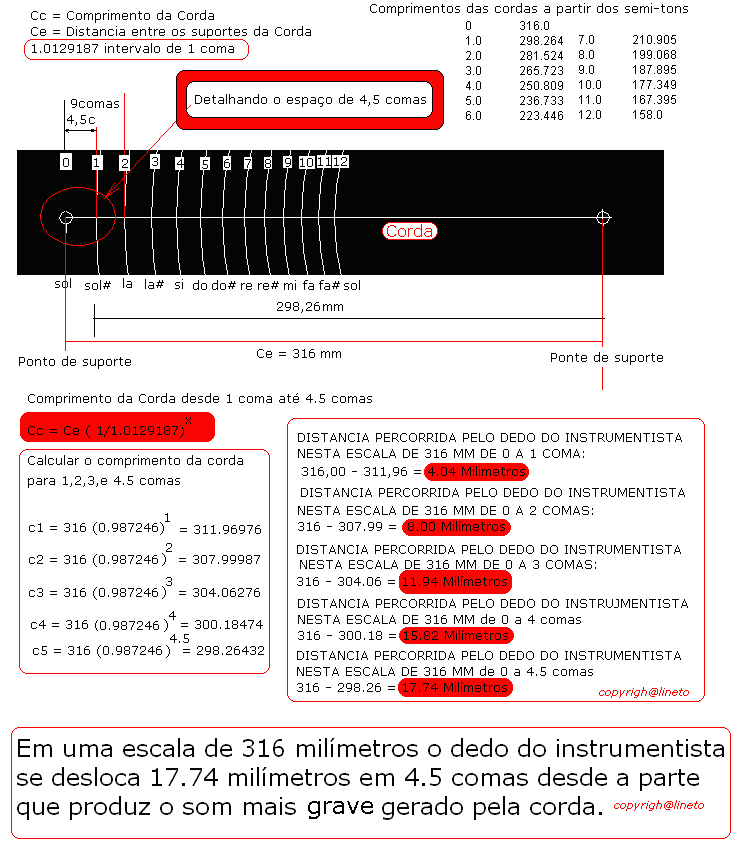
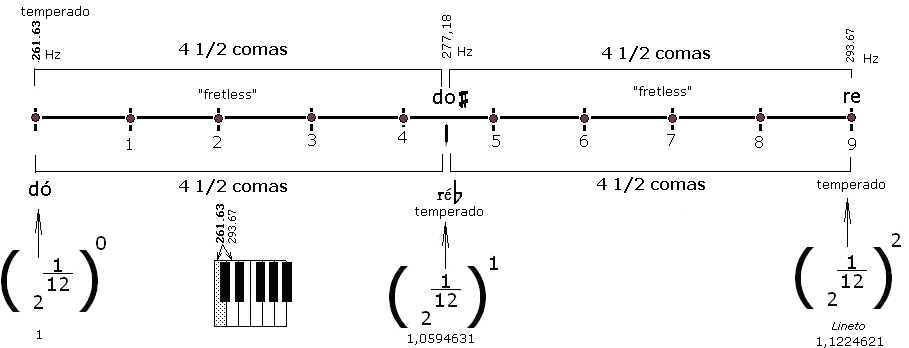
por: Prof.Luiz Netto Qual o deslocamento do dedo do instrumentista quando percorre uma corda de 316 milimetros de comprimento desde 0 até 4.5 comas? DETALHE AMPLIADO – COMO VARIAM AS DISTÂNCIAS PARA PRODUZIR INTERVALOS MUSICAIS DE 0,1,2,3, 4 e 4 1/2 COMAS. O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil Retornar ao Índice
por: Prof.Luiz Netto Thomas Alva Edison, e uma de suas magnificas invenções – O “phonógrafo”. Quem quer que ja tenha ouvido o som que sai de de uma daquelas antigas vitrolas acústicas deve ter ficado espantado e maravilhado com o volume de som forte que sai daquela magnífica corneta acústica. Nos meus tempos de criança, quando eu ia ao sitio de minha avó em Piquerobi, SP – a única diversão que lá havia era uma dessas vitrolas, bem como um rádio (Marca Belmonte) – cuja fonte era uma enorme pilha que era trocada mais ou menos a cada 4 ou […]
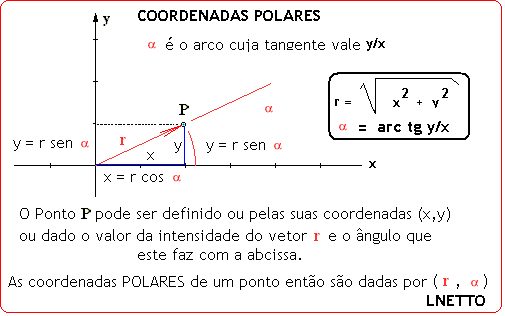
por: Prof.Luiz Netto Assim se temos (r, alfa), imediatamente podemos transformar as coordenadas desse ponto dada em coordenadas polares para coordenadas cartesianas: Seja r = 5 e alfa = 25 graus, então: y = r.sen(alfa)-> y = 5.sen 25 -> y = 5.0,4226182 -> y = 2,113091 x = r cos (alfa) -> 5.cos 25 -> x = 5.0,9063077 -> x = 4,5315385 ou fazendo o inverso, se temos as coordenadas x e y e queresmos as coordenadas polares: Seja: x = 4,5315385 y = 2,113091 e queremos expressar as coordenadas cartesianas desse ponto em coordenadas polares: Qual é o […]
por: Prof.Luiz Netto Na tabela acima vemos que as notas musicais podem ser representadas em notação polar, associando ao valor de cada nota um ângulo.Como temos em uma circunferência 360 graus ou 2 pi radianos, e temos na escala musical temperada doze intervalos, a cada intervalo de meio tom (100 cents) – corresponderá 30 graus, ou pi/6 radianos. O problema que nos propomos a resolver é dado um desses valores, calcular o ângulo que lhe corresponde: Seja o problema: Sabemos que o valor da nota é igual a 1.4983071 que corresponde à nota Sol, qual é o ângulo que está […]
por: Prof.Luiz Netto Quando se estuda o dimensionamento das distâncias entre os trastes dos instrumentos musicais de cordas, calcula-se matemáticamente onde deve ficar os trastes e parece que está tudo resolvido, é só pontear as cordas em determinadas posições e ter-se-à o som matematicamentete calculado, com a frequência determinada. Só que as coisas não acontecem exatamente assim. E porque? Por uma razão muito simples de se entender. Olhando a para a figura situada logo mais abaixo você vai entender o porque. Ao se aplicar o dedo sobre a corda exerce-se sobre esta uma sobretensão. Ora, o instrumento havia sido afinado […]
por: Prof.Luiz Netto Pontos comuns com a escala temperada – Cálculos No sistema temperado os intervalos são iguais. Coma é um intervalo musical. O intervalo de 1 tom compreende os intervalos de 9 comas. Portanto no sistema igualmente temperado ao intervalo de 1/2 tom corresponde ao intervalo de 4 e 1/2 comas. O intervalo coma é obtido dividindo o “espaço” de um tom em 9 intervalos. Portanto as notas musicais obtidas nestes intervalos só são possiveis de serem executadas nos instrumentos “fretless” ou seja nos instrumentos que não tem trastes pois nestes os intervalos são de meio em meio tom. […]
por: Prof.Luiz Netto Unidades de Medidas O Cent – O Savart O cent e o savart são unidades de medidas que permitem medir intervalos sonoros bem pequenos. A percepção da menor variação em frequência detectada pelo ouvido varia ao longo da faixa de áudio. O ouvido é bastante sensível aos sons graves e tem sua sensibilidade máxima entre 3,5 e 4.0 Khz, muito próximo da primeira zona de ressonância que ocorre no ouvido externo. A segunda zona de ressonância ocorre próximo aos 13 Khz. A capacidade de distinção do ouvido em relação à menor variação de frequência, depende da frequência […]
