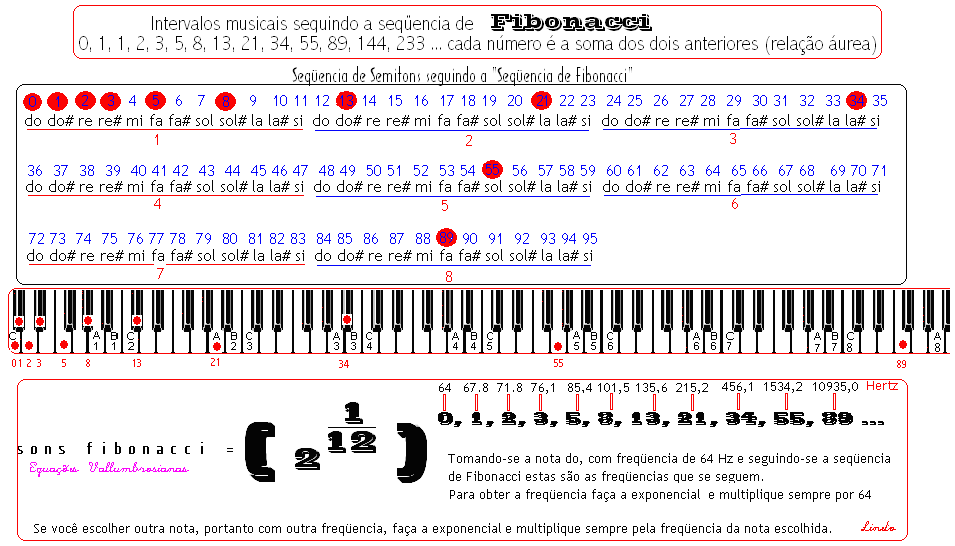
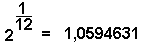O,1,1,2,3,5,8,13,21,34,55,89,144,233… por: Prof.Luiz Netto Os números de Fibonacci plotados na espiral musical Referência: B.Vallumbrosius – Equações Vallumbrosianas (1861-1928) O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil Retornar ao Índice
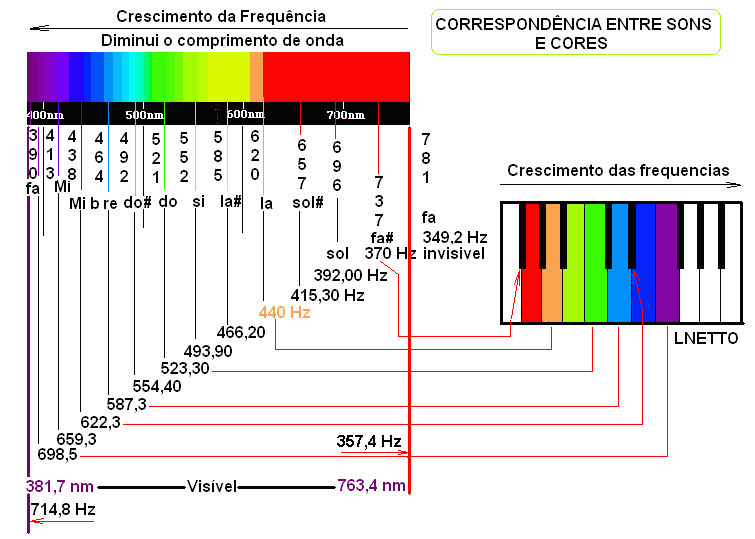
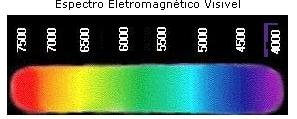
Relacionando as frequências entre Notas Musicais e da Luz Visível por: Prof.Luiz Netto Os sons e as cores A natureza dotou o homem dos sentidos mínimos que precisa para orientar-se: visão, audição, olfato, tato, paladar, de modo que com o concurso de todos eles, possa sentir o cheiro e o sabor das coisas, possa andar sobre a terra, detectando os perigos existentes, sentir onde está os alimentos, defender-se de um ataque iminente detectado, podendo assim resguardar o seu dom mais precioso que é a vida. Com relação ao sentido da audição, é interessante notar que inicialmente ouve-se as frequências, em […]
O Telefone Sem Fio de Landell de Moura Um Invento precursor do Cinema Falado por: Prof.Luiz Netto A LUZ TRANSPORTANDO A INFORMAÇÃO DO SOM Representação esquemática de um projetor No projetor de imagens de cinema faz-se simultaneamente a projeção das imagens e a leitura ótica dos sons impressos fotograficamente na trilha sonora. Existe um sincronimo entre a imagem e o som. Os fotogramas de uma película, diferindo ligeiramente um do outro, vendo-se do lado esquerdo da película a trilha sonora onde os tons de cinza ao negro, variam em frequencia de acôrdo com o sinal de audio gravado. Como variam […]
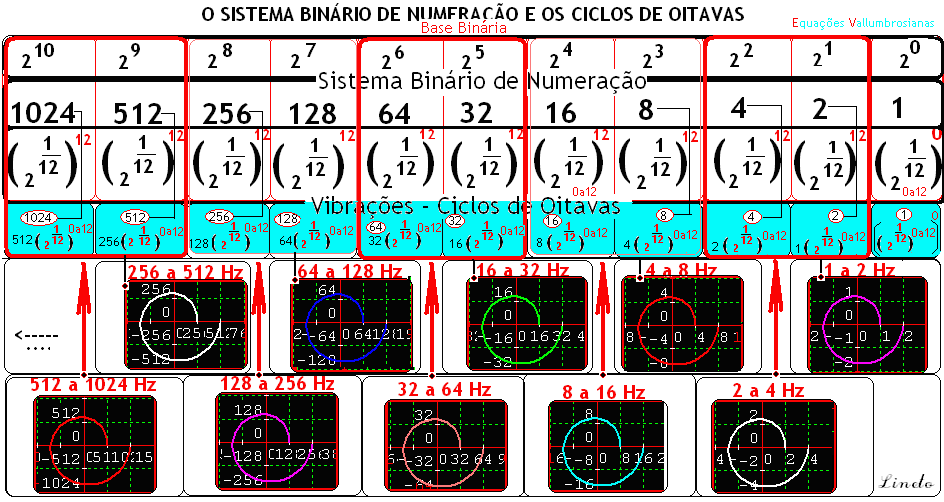
por: Prof.Luiz Netto A frequencia inicial e final do ciclo de uma oitava do espectro oscilatório coincide com uma posição relativa do sistema binário de numeração, como podemos ver na figura a seguir: Consultas e Referências: Equações Vallumbrosianas Bernardus Vallumbrosius (1861-1928) O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil Retornar ao Índice
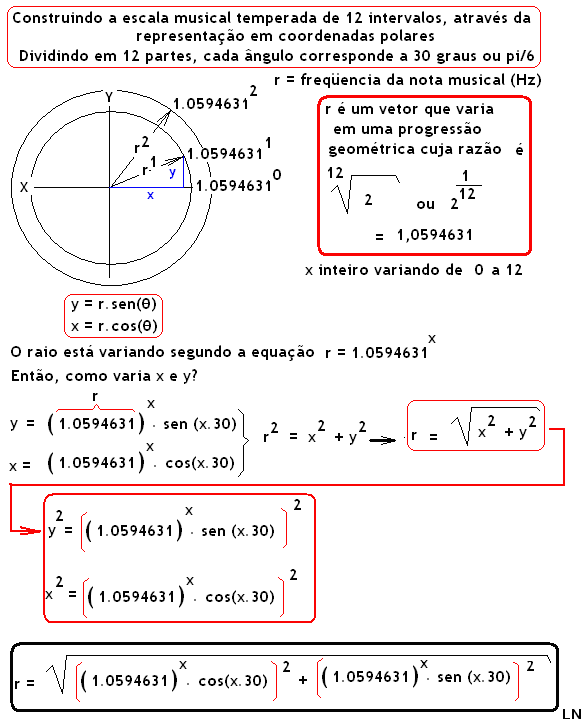
(Vallumbrosius) por: Prof.Luiz Netto EXEMPLO DE CÁLCULO DE r x=1,ângulo de 30 graus ou pi/6 EXEMPLO DE CÁLCULO DE r x=2,ângulo de 60 graus ou pi/3 Aplique a fórmula e calcule para os demais valores de x -> 0,(1)(2),3,4,5,6,7,8,9,10,11 e 12. ESPIRAL LOGARÍTMICA REPRESENTATIVA DA ESCALA MUSICAL TEMPERADA GERANDO A ESPIRAL DA ESCALA MUSICAL TABELA GERADA PELA EQUAÇÃO ACIMA CINCO OITAVAS Para calcular as frequencias das notas musicais, começando pelo dó medio do piano, por exemplo,com a frequencia de 261.626 Hz é só ir multiplicando seguidamente pelos números de r1, r2, r3…. r12, ou multiplicar seguidamente por 1.0594631. Repare que […]
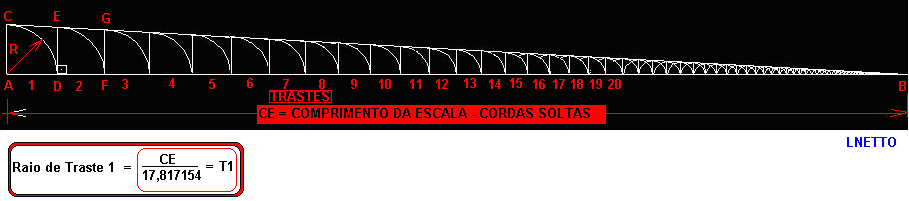
por: Prof.Luiz Netto Utilizando sómente uma regua e compasso podemos também determinar a posição dos trastes ao longo do braço do instrumento. A única conta que precisamos fazer é aquela indicada acima, ou seja dividir o comprimento da escala – (CE) – por 17,817154 e aí temos o valor do traste 1. Traça-se pelo ponto A uma circunferência cujo raio corresponda ao valor calculado. Traça-se uma perpendicular à reta AB, que intercepta a circunferência de raio R, no ponto C. Une-se o ponto C com B, obtendo-se o triângulo ABC,. A partir daí traça-se uma perpendicular por AB no ponto […]
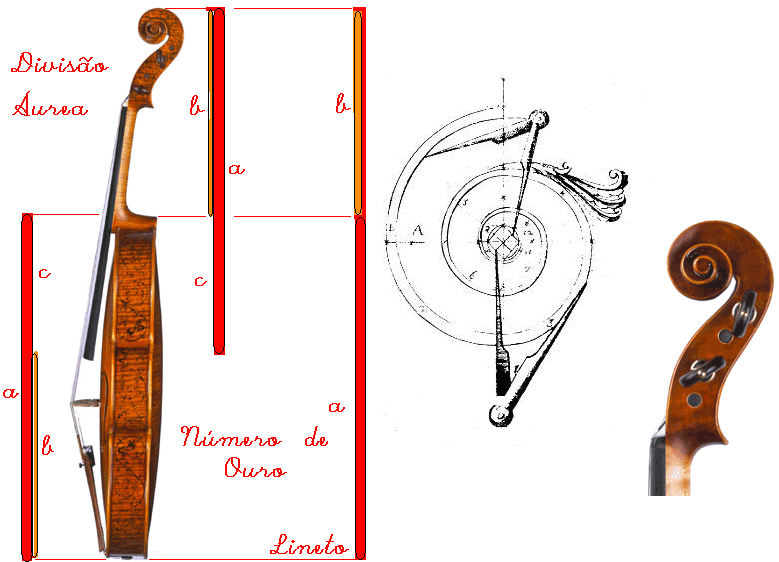
por: Prof.Luiz Netto Não há como negar a beleza do instrumento violino. Parece que nós seres humanos percebemos a beleza ou sentimos a beleza de uma forma quando segue um padrão ou algo que não sabemos definir, que está embutido em nosso ser, provavelmente porque esta forma mantém relações em suas linhas que nos causam essa sensação do belo. Assim, um violino é uma dessas peças. Quando o violino foi criado a estética das proporções foi objeto de preocupação de vários artistas. Alguns violinos foram criados a partir do que foi chamado “O Número de Ouro” e em suas linhas […]
por: Prof.Luiz Netto Quando no estudo da matemática nos deparamos com algum tópico que podemos visualizar uma aplicação prática, e para nossa felicidade, há muitos deles, se já apreciamos o seu estudo, isto reforça ainda mais nosso interesse, pois afinal aquilo que é produto exclusivo da inteligência do homem, a matemática, encontra um modelo prático que represente o que era produto da inteligência, da imaginação. Assim, quando estudamos a matemática da música, em seus vários aspectos, como por exemplo, na análise das sequências das notas sonoras da escala musical igualmente temperada, nos damos conta que os valores das frequências das […]
por: Prof.Luiz Netto Os símbolos empregados na pauta musical para abarcar toda a tessitura dos instrumentos musicais tem variado ao longo do tempo sendo atualmente empregado os símbolos para a clave de Sol, para a clave de dó e para a clave de Fá. É curioso verificar que houve uma modificação paulatina ao longo do tempo introduzida pelos copistas de partituras, até que chegassem a essa representação nos dias de hoje, talvez na tentativa de simplificar os traços e conferir maior rapidez no desenhar. É intrigante verificar que todas elas trazem algo em comum dentro de seus traços: Algo que […]
por: Prof.Luiz Netto Lendo o título acima alguém pode perguntar: não estaria este titulo equivocado? Bem, acho que não como logo verão neste artigo…Quando refletimos acerca dos fenômenos vibratórios e quais desses são detectados pelos seres humanos vemos que somos dotados de apenas alguns sentidos que detectam apenas alguns fenômenos que ocorrem na natureza. Miríades de outros fenômenos vibratórios permanecem desconhecidos por nossos sentidos.Certamente os sentidos que temos são aqueles mínimos necessários para manutenção, defesa e continuidade da nossa vida e que a natureza nos dotou. Tudo o mais que o homem precisa ele constrói. Se não vemos com nossos […]
por: Prof.Luiz Netto É curioso notar que as frequencias das notas musicais na escala musical temperada tem um comportamento de crescimento semelhante ao cálculo de juros compostos. É só considerarmos que na escala musical temperada de 12 intervalos a taxa de crescimento é de 5,94631%). Aplicando esta fórmula você pode calcular todos os valores das notas musicais da escala musical temperada de meio em meio tom, é só ir variando o expoente de zero à 12, partindo da frequencia de uma nota musical conhecida. O intervalo entre as duas notas aqui calculadas é de uma oitava porque o quociente entre […]
por: Prof.Luiz Netto Para que servem os logaritmos? Entenda-os e descobrirá a enorme utilidade deles! Já dizia o físico italiano Galileu Galilei que a Matemática é a linguagem da Física. Uma das percepções mais agudas no campo da Matemática foi a do entendimento do que são os logaritmos, e o vislumbre de muitas aplicações de suas propriedades na descrição de muitos fenômenos da natureza. Só para citar algumas: 1)O valor do Ph das soluções, cuja acidez ou alcalinidade é medida por uma escala Logarítmica.: (Ph) –> pondus hidrogeni –> peso do hidrogênio. Ph = 7 –> (Neutro) –> significa que […]
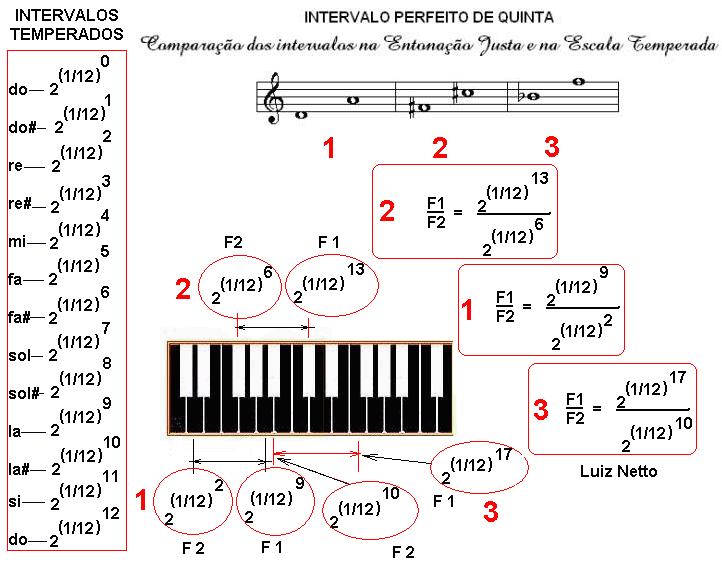
por: Prof.Luiz Netto Para compararmos os intervalos perfeitos de quinta na Entonação Justa e na Escala Temperada, onde a razão entre os quocientes de duas frequências adjacentes são sempre iguais entre si, é necessário calculá-los em unidades denominadas “Cents“, que se obtém aplicando a fórmula seguinte: Portanto, vamos aplicar essa fórmula para calcular em “Cents” o tamanho do intervalo perfeito de quinta na escala musical temperada e também para o mesmo intervalo na entonação justa e verificar a grandeza dos dois intervalos. NA ESCALA TEMPERADA NA ENTONAÇÃO JUSTA Portanto vemos que o intervalo perfeito de quinta na escala temperada é […]
por: Prof.Luiz Netto Nota: Este estudo (Representação Polar da Escala Musical) é algo que não encontrei até hoje tanto em livros como na internet. Nunca encontrei esta equação que estou utilizando: r = (1.0594631)^(1.9098593t). (Notação utilizada nos programas de geração de gráficos). Encontrei algo sugerindo a ideia dessa espiral logarítmica para representar as oitavas musicais, mas que o autor não saberia qual a equação que poderia descrevê-la. Estudando-a, eu a desenvolvi. Claro está que a maneira tradicional de representação é uma maneira simbólica muito boa. – O que pretendemos é descrever matematicamente a sequencia de quintas e claro podemos fazer […]
por: Prof.Luiz Netto Regência Matemática na Música Tabelando as Relações Escala Cromática com 12 intervalos iguais – Escala Temperada Escala Cromática com 12 intervalos de razão 16/15 Verifique que estes intervalos produzem uma oitava mais alta que 2*(261,6)=523,2 Comparações O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil Retornar ao Índice