Crossovers

por: Álvaro Carvalho de Aguiar Neiva

De tempos em tempos alguém me procura com o mesmo problema: ” …qual o valor do capacitor que devo colocar em série com o tweeter (ou o driver da corneta) das minhas caixas acústicas para que ele pare de queimar ? “.

Esta é uma questão embaraçosa, uma vez que não há uma resposta direta satisfatória (veremos porque adiante) e o mais correto será alertar para a necessidade do uso de um divisor de freqüências (crossover) adequado.

Como argumento para justificar o custo maior de um divisor, poderemos pegar o preço de um reparo e calcular em quanto tempo recuperaremos o investimento.

Para lançar um pouco de luz sobre o assunto (assim espero), vamos primeiro ver o que são e porque utilizamos os divisores de freqüência e depois analisar uma realização comercial dos mesmos com suas dificuldades práticas de uso e construção. Vou procurar atingir as pessoas que têm aquele tipo de dúvida que citei no início e por isto precisarei explicar alguns conceitos básicos.

1 – O que é freqüência:

Todos os sons que percebemos são flutuações da pressão do ar acima e abaixo de um valor médio. Chamamos de freqüência ao número de alternações (ciclos) que ocorrem por segundo e a percepção subjetiva que temos desta característica física é que nos permite identificar um som de alta freqüência como agudo e um de baixa freqüência como grave e perceber os diferentes tons de uma escala musical. A unidade de medida da freqüência é o Hertz (Hz), igual a um ciclo por segundo (1 c/s). Utilizamos freqüentemente em áudio o quilohertz (kHz), o múltiplo da unidade de freqüência igual a 1000 Hz ou 1000 c/s. Se a razão entre as freqüências de dois sinais for igual a 2 (f2/f1 = 2, ou seja f2 = 2.f1), dizemos que os mesmos estão separados por uma oitava.

2 – Porque utilizar um divisor de freqüências?

Não existe um alto-falante capaz de reproduzir adequadamente toda a faixa audível de sinais (20 Hz a 20.000 Hz ou 20 kHz), especialmente em altos níveis de pressão sonora. Como as exigências de projeto dos transdutores (alto-falantes) de altas (tweeters ou drivers) e baixas freqüências (woofers) são conflitantes, costuma-se dividir a faixa de áudio em duas ou mais partes e usar transdutores otimizados para cada uma delas. Por outro lado, o envio de sinais fora da faixa adequada a um alto-falante só irá produzir calor e distorção, aumentando a possibilidade de danos ao mesmo.

Caberá ao divisor de freqüências (crossover) a separação dos sinais a serem enviados a cada alto-falante.

3 – O que são os divisores de freqüência?

São filtros elétricos que separam os sinais a serem enviados a cada transdutor em função de sua freqüência e podem ser divididos em duas grandes classes, de acordo com a potência dos sinais que manejam:

a) divisores de alto nível, que lidam com potências elevadas e são usados entre os amplificadores de potência e os alto-falantes. São construídos com indutores, capacitores e resistores, sendo portanto redes passivas que entregam sempre menos potência à carga do que recebem do amplificador. Por isto, também são conhecidos como divisores passivos.

b) divisores de baixo nível, utilizados antes dos amplificadores de potência, em sistemas multi-amplificados. Geralmente são construídos com amplificadores operacionais e redes RC (resistores e capacitores). Por este motivo também são conhecidos como divisores ativos.

Vamos analisar neste artigo os divisores passivos. Eles são usados na maioria dos sistemas de reprodução de áudio por serem eficientes e econômicos em termos de quantidade de componentes e permitirem o uso de apenas um amplificador para alimentar um par de caixas acústicas com duas, três ou mais vias. Temos ainda o benefício adicional da proteção inerente dos drivers de alta freqüência contra falhas na amplificação que coloquem corrente contínua ou baixas freqüências na saída do amplificador de potência.

Por outro lado, a combinação crossover/alto-falantes pode representar uma carga difícil para o único amplificador de potência encarregado de fornecer a energia para todos os alto-falantes, podendo mesmo sobrecarregá-lo se não forem tomados os devidos cuidados. Este fato, somado às perdas que ocorrem nos indutores colocados em série com os woofers, torna atraente o uso dos sistemas multi-amplificados com divisores ativos para os sistemas de alta potência e elevado desempenho, como os utilizados em shows ao ar livre, por exemplo.

4 – Como os crossovers separam os sinais em função de sua freqüência?

São usados circuitos chamados de filtros elétricos, os quais deixam passar as freqüências desejadas e atenuam as indesejáveis.

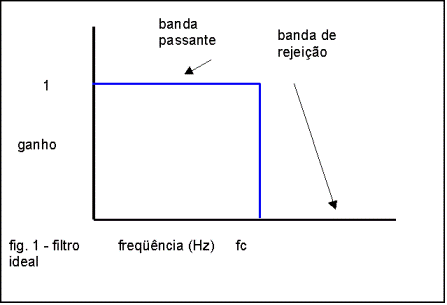
Podemos observar na fig. 1 um gráfico que representa a ação de um filtro ideal: deixa passar sem nenhuma atenuação as freqüências até fc, a chamada freqüência de corte, e rejeita completamente todas as outras freqüências. As freqüências até fc definem a banda passante e as que são rejeitadas a banda de rejeição do filtro. Um filtro descrito por um gráfico como este não é realizável fisicamente e um filtro real somente conseguirá aproximar o seu comportamento. O ganho G do filtro é dado pelo quociente entre a tensão sobre a carga e a tensão da fonte, e o ganho em dB é dado por vinte vezes o logaritmo de G.

Apresentamos o gráfico da resposta de freqüência de um filtro normalmente com o ganho em dB no eixo y (ordenadas) e a
freqüência no eixo dos x (abscissas), em escala logarítmica.

Quando as freqüências rejeitadas estão acima da freqüência de corte (f>fc), temos um filtro do tipo passa-baixas (PB).

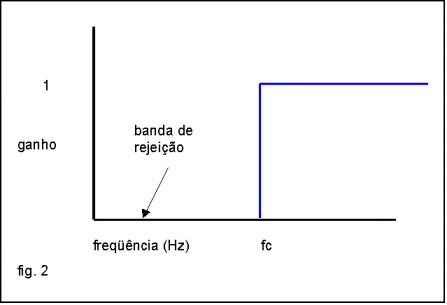
Podemos ter também filtros passa-altas , se rejeitarmos freqüências abaixo de fc (fig. 2) ou passa-banda se a faixa passante estiver entre duas freqüências f1 e f2 (fig. 3).

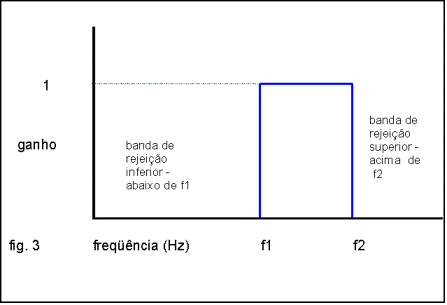
Um filtro real atenua gradualmente as freqüências fora da faixa passante e o gráfico resultante tem uma inclinação medida em dB/oitava ou dB/década, como o filtro de 2ª ordem passa-baixas mostrado na fig. 4.

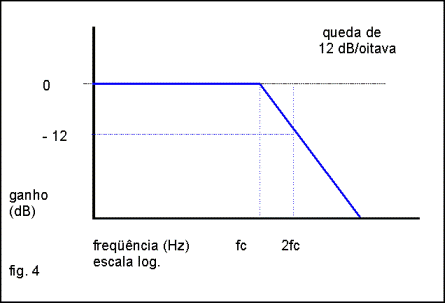
Para conseguirmos a seletividade desejada em função da freqüência, lançaremos mão das propriedades dos indutores e capacitores.

5 – O que são resistores, indutores e capacitores?

Capacitores (C)

Olhando um crossover montado, podemos identificar os capacitores pela presença da indicação de seu valor (geralmente em microfarads (mF)) e sua tensão de isolamento em V. Capacitores são formados por um sanduíche de duas placas condutoras separadas por um isolante ou dielétrico. Os capacitores armazenam energia sob forma de campo elétrico.

Se aplicarmos uma tensão contínua (uma bateria por exemplo) a um capacitor, este irá carregar-se até o valor da tensão da fonte, drenando uma corrente limitada apenas pela resistência que houver entre a fonte e o capacitor, e, após este instante, não circulará corrente pelo circuito, parecendo o capacitor um circuito aberto. Por isto é que eles são úteis como proteção para os drivers e tweeters contra falhas nos amplificadores de potência.

Se aplicarmos ao capacitor uma tensão alternada cuja forma de onda seja como a da fig. 5 (como vista em um osciloscópio), uma tensão que chamamos de senoidal, vamos observar uma coisa interessante: após algum tempo, circula uma corrente que possui a mesma forma mas com amplitude diferente e um deslocamento no tempo que faz com que os máximos e mínimos da corrente correspondam às passagens por zero da tensão (fig. 6). Chamaremos a este deslocamento de defasagem ou simplesmente fase, medido em graus ou radianos.

Fig. 5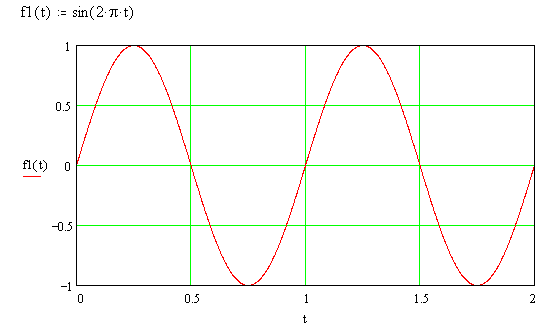

Os capacitores armazenam energia no campo elétrico que aparece entre as cargas que se acumulam em suas placas, e por isso, primeiro aparece a corrente (acumulando cargas) para que possa surgir a tensão, e a defasagem introduzida será de +90º (fig. 6).

Fig. 6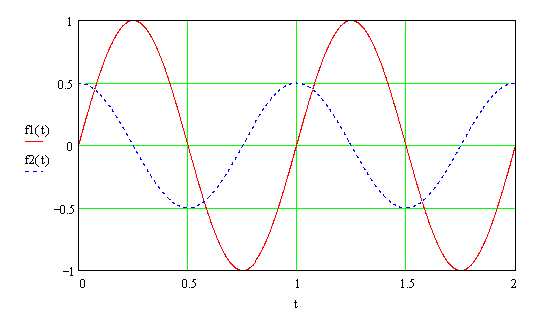

Assim, para sabermos a relação entre tensão e corrente (alternadas e senoidais) em um capacitor, ou seja, sua impedância , precisaremos de dois números: magnitude e fase , a fase será de 90º e a magnitude será dada pela expressão (1)

X_c = 1/ 6,28.f.C (1)

onde X_c é a magnitude da impedância do capacitor ou reatância, dada em Ohms (W), f é a freqüência em Hz e C a capacitância em Farads (F). Observando a expressão (1) acima, vemos que a impedância (reatância) do capacitor decresce com a freqüência, tendendo a zero (curto-circuito) para altas freqüências e para infinito (circuito aberto) quando f tende a zero (CC). Se fizermos as contas, Xc reduz-se à metade quando f dobra, ou seja, sobe uma oitava, ou dito de outra forma, Xc decresce a uma taxa de 6 dB / oitava.

Indutores (L)

Indutores são bobinas de fio enroladas em torno de um núcleo, geralmente de ar (nos divisores) e têm um comportamento oposto ao dos capacitores, ou melhor dizendo, dual . Neles, tensão e corrente tem papéis trocados em relação ao capacitor, ou seja, se aplicarmos uma tensão contínua a um indutor ideal, ele se comportará como um curto-circuito! Analogamente, eles possuem uma impedância dada por uma expressão que é o inverso da obtida para os capacitores, e uma defasagem de – 90º (fig. 7). Assim, teremos para o indutor:

X_l = 6,28.f.L (2)

onde X_l é a magnitude da impedância do indutor, dada em Ohms (W), f é a freqüência em Hz e L a indutância em Henries (H).

Fig. 7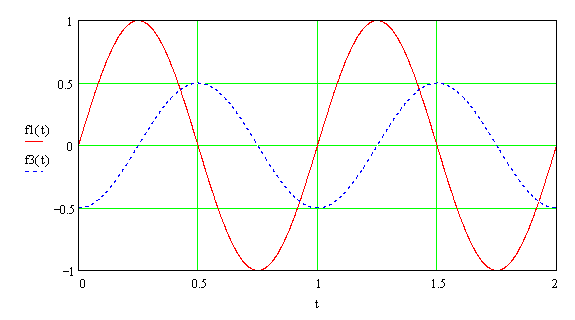

Observando a expressão (2) acima, veremos um comportamento exatamente oposto ao do capacitor:

X_l cresce com a freqüência, tendendo a zero (curto-circuito) para baixas freqüências e para infinito (circuito aberto) quando f cresce, a uma taxa de 6 dB/ oitava. Os indutores armazenam energia sob forma de campo magnético.

Resistores

Os resistores não armazenam energia, mas a dissipam sob forma de calor, e isto faz com que tensão e corrente estejam em fase neles. Para sabermos a relação entre tensão e corrente em um resistor precisamos apenas de
um número, a sua resistência elétrica(V/A), também medida em Ohms.

Atenção para a fase! Vimos anteriormente que capacitores e indutores introduzem defasagens entre tensão e corrente e isto pode causar uma série de problemas ao somarmos os sinais que vêm de diferentes filtros. Como podemos observar na fig. 8, caso a defasagem entre dois sinais chegue a 180º, teremos o cancelamento do sinal soma!

Fig. 8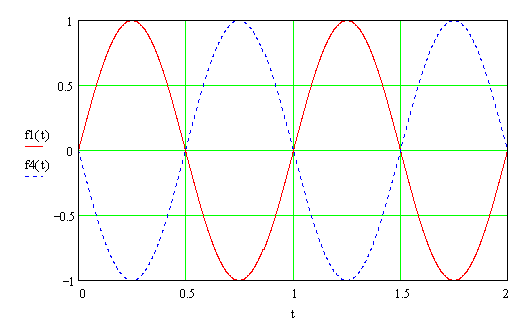

A importância disso tudo é que usando circuitos com indutores e capacitores poderemos selecionar as freqüências que passam para uma carga, como veremos adiante. Poderemos usar os resistores para atenuação ou ajuste da impedância de um alto-falante ou driver. Mostramos na figura 9 a representação esquemática dos capacitores, indutores e resistores que usamos nos divisores de freqüência.

Fig. 9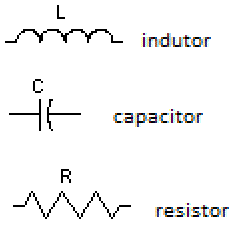

Fig. 10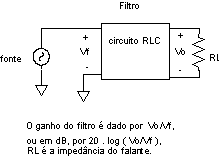

Mostramos de uma forma esquemática na fig. 10 um filtro colocado entre uma fonte de sinal (um amplificador de potência por exemplo) e uma carga. O problema será escolher os componentes que estarão dentro do bloco de filtragem e a forma de interligá-los.

Já que iremos atenuar as freqüências que não desejamos, porque não usar uma configuração como a do atenuador resistivo mostrado na fig. 11? Quando usamos resistores, a atenuação obtida será independente da freqüência, mas, se substituirmos um dos dois resistores (ou ambos) por uma impedância dependente da freqüência (fig. 12), passaremos a obter uma atenuação que irá aproximar as características de filtragem que desejamos.

Fig. 11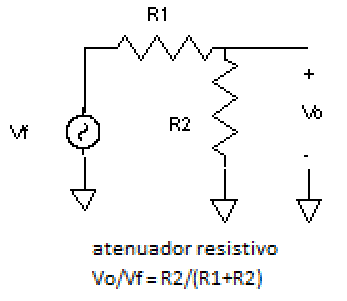

Fig. 12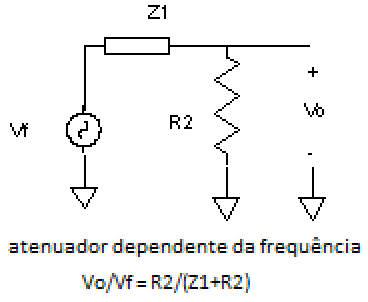

O que é a ordem de um filtro?

Embora exista uma definição precisa do que seja a ordem de um circuito elétrico, ela está fora do escopo deste artigo, e uma consulta a um livro sobre teoria de circuitos será mais adequada. Felizmente, para nossos propósitos e para a maioria dos circuitos usados em divisores de freqüência, poderemos considerar a ordem do circuito como o número total de capacitores e indutores do mesmo.

O que nos interessa é que a ordem do filtro está intimamente relacionada com a rapidez com que ele rejeita as freqüências indesejáveis. Assim, um filtro de 2ª ordem atenua mais rapidamente os sinais fora de sua faixa de passagem do que um de 1ª , um de 3ª ordem mais que um de 2ª e etc.. Por outro lado, quanto maior a ordem de um filtro, mais capacitores e indutores teremos que utilizar e maior será a defasagem introduzida pelo filtro perto da freqüência de corte.

A taxa de atenuação dos filtros mais usados em divisores (tipo Butterworth) será proporcional à sua ordem, assim, os filtros de 1ª ordem terão uma taxa de 6 dB/oitava, os de 2ª ordem 12 dB/oitava e os de 3ª ordem 18 dB/oitava. De uma forma geral a inclinação dos gráficos será de 6n dB/ oitava, onde n é a ordem do filtro.

Sistemas

Quando falamos de crossovers, estamos nos referindo a filtros que trabalham em conjunto, de tal forma que a sua soma, incluindo os efeitos dos transdutores, reproduza toda a faixa que conste das especificações da caixa acústica. Para conseguir isto, precisamos tomar cuidado com a combinação entre as diversas seções do crossover.

Vias

Dividimos o espectro de sinais de áudio em duas ou mais bandas ou faixas e usamos os filtros adequados para separar os sinais e alimentar os alto-falantes de cada faixa. Costumamos chamar de vias às diversas saídas do divisor de freqüências. Assim, um sistema com um woofer e um tweeter ou driver de médias e altas freqüências será um sistema de duas vias, que terá um filtro passa-altas para alimentar o driver ou tweeter e um filtro passa-baixas para alimentar o woofer. Caso tenhamos um woofer, um driver ou falante de médios e um tweeter, teremos um sistema de três vias, o que exigirá um filtro passa-banda para a faixa de médios, além dos dois filtros anteriores, e assim por diante.

Divisores de freqüência e filtros são assuntos que demandam uma base bastante forte em análise e síntese de circuitos e um tratamento mais aprofundado iria fugir completamente ao escopo deste artigo. O leitor interessado no assunto deverá consultar o livro Caixas Acústicas e Alto-Falantes, tradução do Loudspeaker Design Cookbook de Vance Dickason por Homero Sette Silva, onde irá encontrar uma excelente apresentação dos diversos tipos de filtros usados em divisores de freqüência, junto com tabelas e fórmulas para calculá-los e construí-los.

Vamos agora examinar alguns casos comuns para divisores de duas vias

Divisor de 1ª ordem

É o mais simples possível e soma muito bem as seções passa-altas e passa-baixas, mas tem rejeição insuficiente das freqüências indesejáveis.

Fig. 13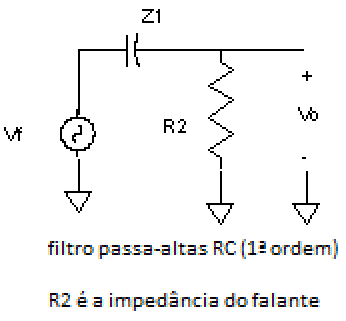

Ao colocarmos um capacitor em série com um tweeter tentamos realizar um filtro passa altas de 1ª ordem (opa!), trocando em miúdos: procuramos atenuar as baixas freqüências que iriam destruir em segundos o diafragma do pobre tweeter, usando apenas um único componente cuja impedância varia com a freqüência.

Desvantagens :

a) a taxa de atenuação é muito suave, caindo 3 dB na freqüência de corte e tendendo a uma queda de 6 dB / oitava, enquanto a excursão do diafragma de um falante dinâmico cresce a mais que 6 dB / oitava, (a taxa exata e a forma da variação dependendo do tipo de
caixa, para obter uma mesma pressão sonora) acima de sua freqüência de ressonância. Por esta, entre outras razões, as caixas acústicas profissionais de alta potência utilizam filtros com atenuação de 12 dB / oitava ou maior. Exemplificando: vamos supor que um determinado tweeter tenha uma freqüência de corte inferior de 2500 Hz. Se aplicarmos um sinal com componentes de igual amplitude em 2500 Hz e 1250 Hz, o componente de 1250 Hz provocará uma excursão mais de 2 vezes maior (ou 6 dB maior), logo precisaremos de uma atenuação mais de 2 vezes ou 6 dB neste intervalo de 1 oitava (2500/1250 = 2).

b) estamos considerando a impedância do tweeter como puramente resistiva e constante, e isto não é verdade e pode ocasionar desvios entre a freqüência de corte calculada e a realmente obtida.

Fig. 14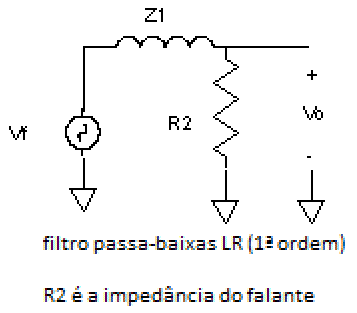

Se não tivermos um indutor em série com o woofer, teremos uma resposta de freqüência candidata a ter muitas irregularidades na faixa de freqüências próxima à região de cruzamento entre o woofer e o tweeter. O filtro passa-baixas de 1ª ordem será exatamente isto (um indutor em série com o woofer), tendo principalmente as desvantagens descritas em b) acima.

Divisor de 2ª ordem

É o mais empregado nos equipamentos em produção comercial, combinando uma boa rejeição das freqüências indesejáveis com um número reduzido de componentes. Podemos conseguir resultados muito bons empregando-o corretamente. Não podemos esquecer que provoca um inversão de fase entre as seções passa-altas e passa-baixas (explico adiante).

Fig. 15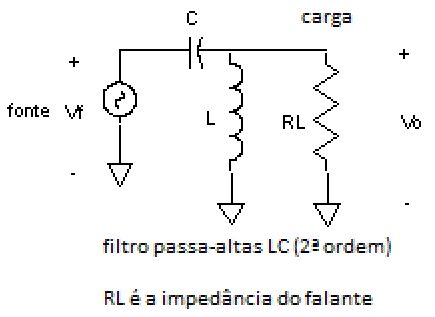

Agora iremos utilizar dois elementos cujas reatâncias variam com a freqüência: um capacitor e um indutor, conseguindo uma atenuação muito mais rápida em função da freqüência – 12 dB / oitava. Como inconveniente, os dois elementos reativos introduzem uma defasagem total de 90° na freqüência de corte fc, em cada seção, o que leva a um total de 180° de defasagem na soma das duas seções, e obriga a inverter a fase do tweeter ou driver em relação ao woofer para evitar o cancelamento de freqüências próximas à fc.

Fig. 16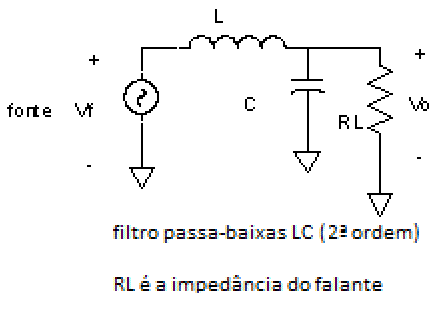

Aqui, mais uma vez capacitor e indutor trocam de papel (não por acaso), fato que vai repetir-se em todas as configurações daqui para a frente.

Divisor de 3ª ordem

Fig. 17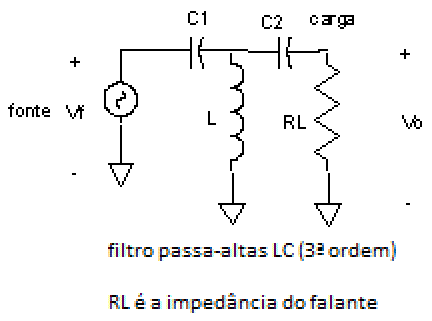

Fig. 18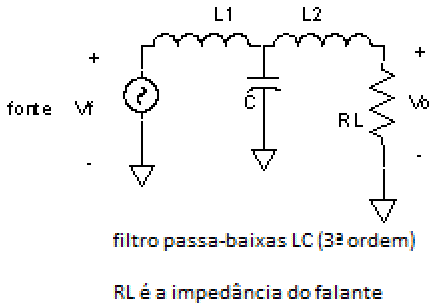

É uma boa opção, quando podemos tolerar um maior número de componentes, já que conseguiremos uma atenuação de 18 dB / oitava e uma soma satisfatória, embora também seja usual uma inversão de polaridade para otimizar o resultado final. É a opção mais econômica para um desempenho superior à média.

Divisor de 4ª ordem (passivo)

Possui um corte rápido (24 dB / oitava) e não necessita da inversão de polaridade em nenhum transdutor para uma soma adequada, mas a sua elevada complexidade (dois indutores e dois capacitores por cada seção passa-altas/passa-baixas) torna-o uma escolha viável apenas em casos muito especiais, onde o custo não seja uma grande objeção.

Mostramos na fig. 19 uma comparação entre as respostas em freqüência de filtrosde 1ª, 2ª e 3ª ordem, com 6, 12 e 18 dB/oitava de inclinação.

Fig. 19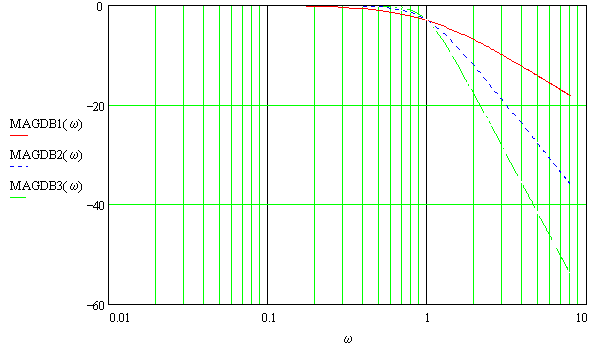

Já a fig. 20 mostra a superposição entre os filtros passa-baixas e passa-altas de um divisor de 2ªordem de duas vias, sendo que fc = 1kHz, para ambas as seções; o gráfico está em dB e kHz.

Fig. 20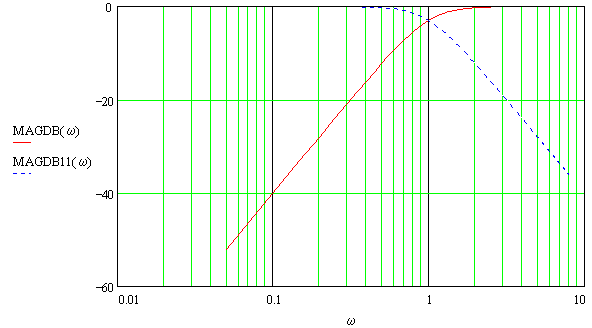

Um caso real

Aplicamos um divisor de duas vias (corte em 4,4 kHz) para estender a resposta de freqüência de uma caixa acústica existente, que utilizava um driver de médios e dois woofers, em uma configuração biamplificada, com o uso de um divisor eletrônico de freqüências para alimentar as duas vias existentes. O divisor passivo foi colocado após o amplificador da faixa de médios/agudos (1kHz a 20 kHz), passando o driver existente a ser alimentado pela saída passa-baixas e a saída passa-altas a alimentar os tweeters (2 em série, com um resistor de 16
W em paralelo para casamento de impedâncias).

Os resultados foram plenamente satisfatórios, estando o conjunto em funcionamento a algumas semanas, sem maiores problemas.

Não foi nenhuma surpresa para mim quando a mesma pessoa que havia solicitado o cálculo de um capacitor para colocar em série com o tweeter adquiriu um divisor de três vias e retornou entusiasmado: ” … agora consigo equalizar as caixas da igreja e o amplificador não queimou mais fusíveis! …”

---