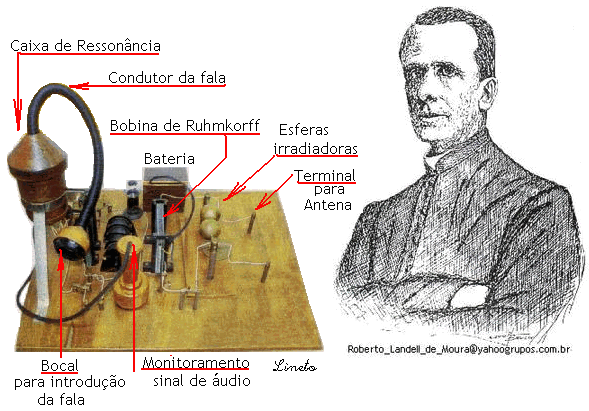
por: Prof.Luiz Netto Quando Landell de Moura construiu o seu TRANSMISSOR DE ONDAS, sabia de suas qualidades e também das limitações técnicas do aparelho e deixou-as muito claramente explicitadas e por isso pediu apoio para continuar os seus estudos que afinal acabaram por não vir. Deixou claro que o aparelho perderia muitos harmônicos contidos nas palavras emitidas, justamente porque os Harmônicos variam em frequência e em amplitude também. Naturalmente ele teria que fixar uma distância entre o ponto de contacto elétrico e o diafragma captador da voz para fechar o circuito do primário da Bobina de Ruhmkorff e por isso […]
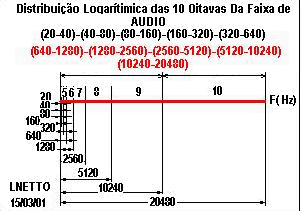
por: Prof.Luiz Netto Parte 1 (*) Antes que possamos chegar aos cálculos para dimensionamento das distâncias dos trastes nos instrumentos musicais de corda, vejamos algumas considerações matemáticas que são indispensáveis sejam feitas para o entendimento de como proceder esse dimensionamento. O nível de conhecimento de matemática exigido para este propósito é que se consiga operar com logarítimos e exponenciais. Se você tem alguma dificuldade para entender a matemática que está por trás deste estudo, não se assuste, aqui há também Tabelas Práticas para consulta. A faixa de audio detetada pelo ser humano está em torno de 10 oitavas, desde 20 […]
por: Prof.Luiz Netto O sábio matemático Bernardus Vallumbrosius, certamente que ao contemplar os valores constituintes da Escala Musical Temperada, notou algumas valôres que lhe pareceram bem familiares como 1,4142 = Raiz Quadrada de 2, – o valor 0,7071 = Raiz Quadrade de 2/2 – (que aparece como uma distância de corda) – e imediatamente se lembrou do Triângulo Retângulo, com dois lados iguais, onde estes valôres aparecem. Intrigado com isso resolveu construir triângulos retângulos cujas hipotenusas tivessem uma sequência constituida pelos números que representam os sucessivos intervalos e viu que os catetos poderiam ser representados também na base 2 elevado […]
Séries de Fourier Seja g(t) uma função periódica de período , definida em IR e integrável, segundo Riemann, em qualquer intervalo limitado. O nosso pressuposto é averiguar se g pode ser ‘expandida’ numa série da forma . (1) Na fórmula acima, é o coeficiente correspondente à função constante , em que o fator está presente por conveniência. O termo não aparece pois . Tendo em conta que e que , a equação (1) pode ser rescrita na forma (2) com e , para cada . Para o que se segue, iremos explorar principalmente (2), contudo devemos também associar os resultados […]
BEDIENT, J., BENT, L., JONES, P., The Historical Roots of Elementary Mathematics, Prentice-Hall Inc., New Jersey, 1976 FOLLAND, Gerald B., Fourier Analysis and its applications, Brooks/Cole Publishing Company, Pacific Groove, California, 1992. HELLEGOUARCH, Yves, “Kreisleriana”, I.R.E.M de Basse-Normandie, Caen, 1985 LOI, Maurice, “Mathématiques et Art”, Hermann, Éditeurs des Sciences et des Arts, Paris, 1995 PAPADOPOULOS, Athanase, Mathematics and Music Theory: from Pythagoras to Rameau, The Mathematical Intelligencer, vol. 24, nº1, Springer-Verlag, New York, 2002 Em formato PDF ou DOC: BARBOSA, Álvaro M., “Edição Digital de Som”, Sebenta do curso de Som e Imagem da Universidade Católica Portuguesa, 1999 URL: http://www.abarbosa.org/docs/edicao_digital_som.pdf […]
No princípio era o som … Na antiguidade foram várias as civilizações que realizaram experiências no campo da acústica. A mais bem sucedida foi a civilização Grega que, por intermédio dos Pitagóricos [1], conseguiu relacionar a acústica com a aritmética. Para tal, muito terá contribuído o papel de relevo desempenhado pela música nas cerimônias gregas assim como os instrumentos por eles utilizados: instrumentos de cordas, sobretudo a cítara, ligados ao culto de Apolo; e os de sopro, sobretudo a flauta, ligados ao culto de Dionísio. Tais instrumentos terão sido bastante sugestivos aos Pitagóricos, pois tanto a cítara, com as suas […]
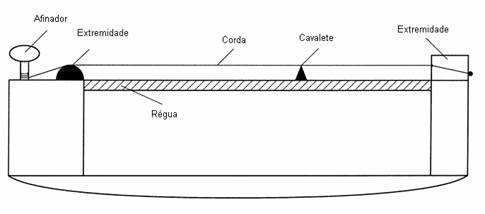
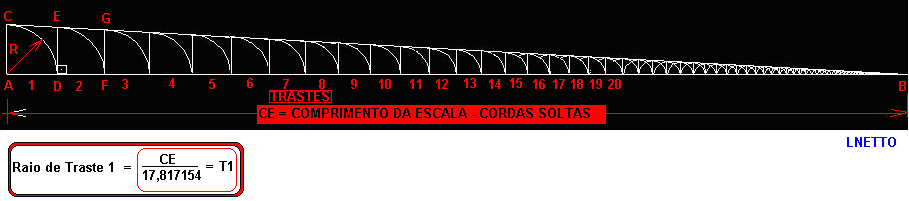
por: Prof.Luiz Netto Utilizando sómente uma regua e compasso podemos também determinar a posição dos trastes ao longo do braço do instrumento. A única conta que precisamos fazer é aquela indicada acima, ou seja dividir o comprimento da escala – (CE) – por 17,817154 e aí temos o valor do traste 1. Traça-se pelo ponto A uma circunferência cujo raio corresponda ao valor calculado. Traça-se uma perpendicular à reta AB, que intercepta a circunferência de raio R, no ponto C. Une-se o ponto C com B, obtendo-se o triângulo ABC,. A partir daí traça-se uma perpendicular por AB no ponto […]
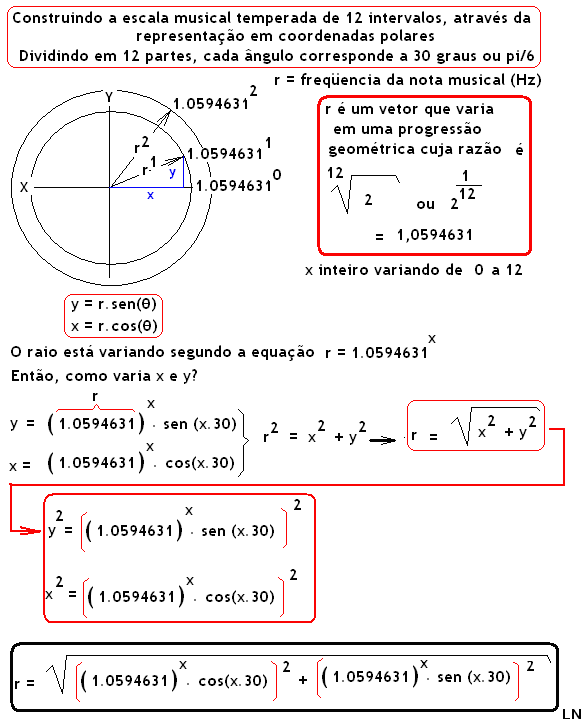
(Vallumbrosius) por: Prof.Luiz Netto EXEMPLO DE CÁLCULO DE r x=1,ângulo de 30 graus ou pi/6 EXEMPLO DE CÁLCULO DE r x=2,ângulo de 60 graus ou pi/3 Aplique a fórmula e calcule para os demais valores de x -> 0,(1)(2),3,4,5,6,7,8,9,10,11 e 12. ESPIRAL LOGARÍTMICA REPRESENTATIVA DA ESCALA MUSICAL TEMPERADA GERANDO A ESPIRAL DA ESCALA MUSICAL TABELA GERADA PELA EQUAÇÃO ACIMA CINCO OITAVAS Para calcular as frequencias das notas musicais, começando pelo dó medio do piano, por exemplo,com a frequencia de 261.626 Hz é só ir multiplicando seguidamente pelos números de r1, r2, r3…. r12, ou multiplicar seguidamente por 1.0594631. Repare que […]
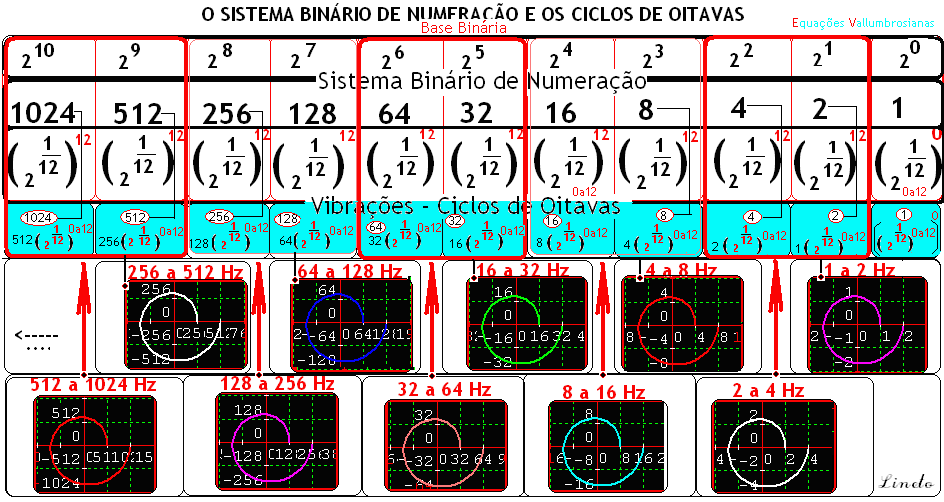
por: Prof.Luiz Netto A frequencia inicial e final do ciclo de uma oitava do espectro oscilatório coincide com uma posição relativa do sistema binário de numeração, como podemos ver na figura a seguir: Consultas e Referências: Equações Vallumbrosianas Bernardus Vallumbrosius (1861-1928) O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil Retornar ao Índice
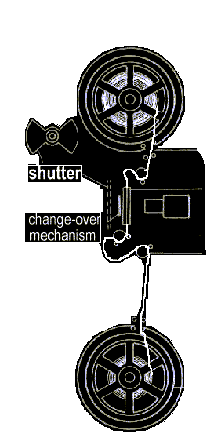
O Telefone Sem Fio de Landell de Moura Um Invento precursor do Cinema Falado por: Prof.Luiz Netto A LUZ TRANSPORTANDO A INFORMAÇÃO DO SOM Representação esquemática de um projetor No projetor de imagens de cinema faz-se simultaneamente a projeção das imagens e a leitura ótica dos sons impressos fotograficamente na trilha sonora. Existe um sincronimo entre a imagem e o som. Os fotogramas de uma película, diferindo ligeiramente um do outro, vendo-se do lado esquerdo da película a trilha sonora onde os tons de cinza ao negro, variam em frequencia de acôrdo com o sinal de audio gravado. Como variam […]
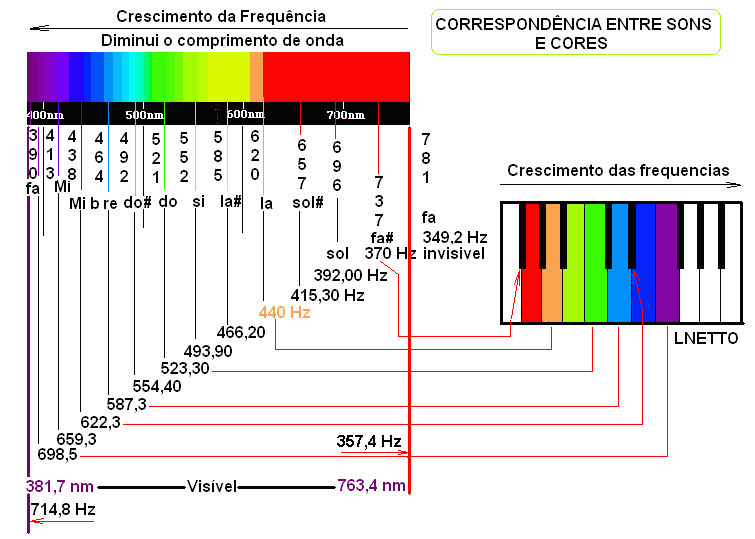
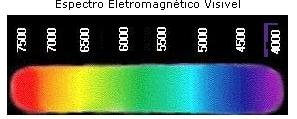
Relacionando as frequências entre Notas Musicais e da Luz Visível por: Prof.Luiz Netto Os sons e as cores A natureza dotou o homem dos sentidos mínimos que precisa para orientar-se: visão, audição, olfato, tato, paladar, de modo que com o concurso de todos eles, possa sentir o cheiro e o sabor das coisas, possa andar sobre a terra, detectando os perigos existentes, sentir onde está os alimentos, defender-se de um ataque iminente detectado, podendo assim resguardar o seu dom mais precioso que é a vida. Com relação ao sentido da audição, é interessante notar que inicialmente ouve-se as frequências, em […]
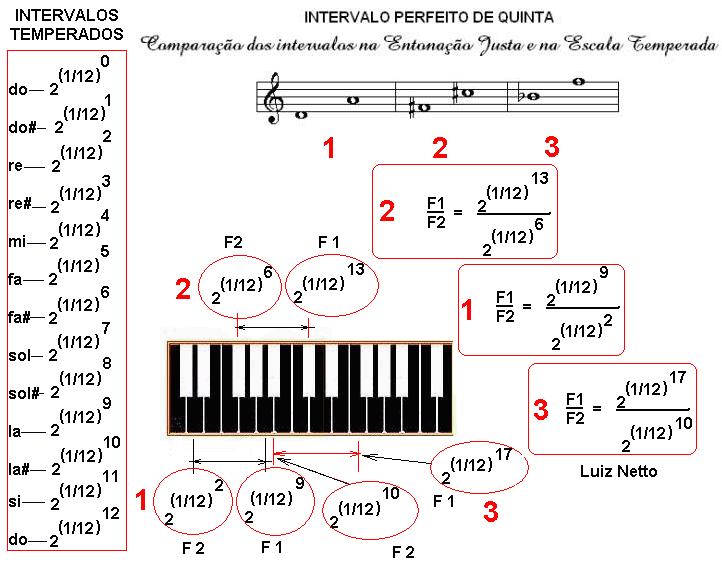
por: Prof.Luiz Netto Para compararmos os intervalos perfeitos de quinta na Entonação Justa e na Escala Temperada, onde a razão entre os quocientes de duas frequências adjacentes são sempre iguais entre si, é necessário calculá-los em unidades denominadas “Cents“, que se obtém aplicando a fórmula seguinte: Portanto, vamos aplicar essa fórmula para calcular em “Cents” o tamanho do intervalo perfeito de quinta na escala musical temperada e também para o mesmo intervalo na entonação justa e verificar a grandeza dos dois intervalos. NA ESCALA TEMPERADA NA ENTONAÇÃO JUSTA Portanto vemos que o intervalo perfeito de quinta na escala temperada é […]
por: Prof.Luiz Netto Para que servem os logaritmos? Entenda-os e descobrirá a enorme utilidade deles! Já dizia o físico italiano Galileu Galilei que a Matemática é a linguagem da Física. Uma das percepções mais agudas no campo da Matemática foi a do entendimento do que são os logaritmos, e o vislumbre de muitas aplicações de suas propriedades na descrição de muitos fenômenos da natureza. Só para citar algumas: 1)O valor do Ph das soluções, cuja acidez ou alcalinidade é medida por uma escala Logarítmica.: (Ph) –> pondus hidrogeni –> peso do hidrogênio. Ph = 7 –> (Neutro) –> significa que […]
por: Prof.Luiz Netto É curioso notar que as frequencias das notas musicais na escala musical temperada tem um comportamento de crescimento semelhante ao cálculo de juros compostos. É só considerarmos que na escala musical temperada de 12 intervalos a taxa de crescimento é de 5,94631%). Aplicando esta fórmula você pode calcular todos os valores das notas musicais da escala musical temperada de meio em meio tom, é só ir variando o expoente de zero à 12, partindo da frequencia de uma nota musical conhecida. O intervalo entre as duas notas aqui calculadas é de uma oitava porque o quociente entre […]
por: Prof.Luiz Netto Lendo o título acima alguém pode perguntar: não estaria este titulo equivocado? Bem, acho que não como logo verão neste artigo…Quando refletimos acerca dos fenômenos vibratórios e quais desses são detectados pelos seres humanos vemos que somos dotados de apenas alguns sentidos que detectam apenas alguns fenômenos que ocorrem na natureza. Miríades de outros fenômenos vibratórios permanecem desconhecidos por nossos sentidos.Certamente os sentidos que temos são aqueles mínimos necessários para manutenção, defesa e continuidade da nossa vida e que a natureza nos dotou. Tudo o mais que o homem precisa ele constrói. Se não vemos com nossos […]