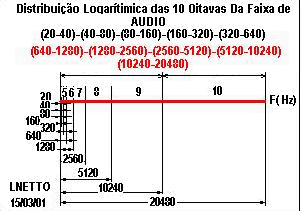
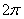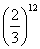por: Prof.Luiz Netto Parte 1 (*) Antes que possamos chegar aos cálculos para dimensionamento das distâncias dos trastes nos instrumentos musicais de corda, vejamos algumas considerações matemáticas que são indispensáveis sejam feitas para o entendimento de como proceder esse dimensionamento. O nível de conhecimento de matemática exigido para este propósito é que se consiga operar com logarítimos e exponenciais. Se você tem alguma dificuldade para entender a matemática que está por trás deste estudo, não se assuste, aqui há também Tabelas Práticas para consulta. A faixa de audio detetada pelo ser humano está em torno de 10 oitavas, desde 20 […]
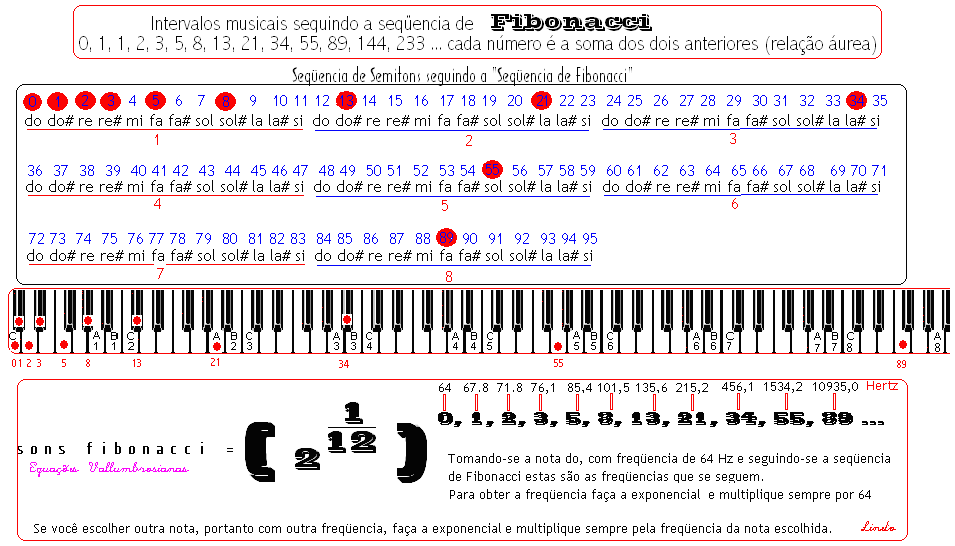
por: Prof.Luiz Netto O sábio matemático Bernardus Vallumbrosius, certamente que ao contemplar os valores constituintes da Escala Musical Temperada, notou algumas valôres que lhe pareceram bem familiares como 1,4142 = Raiz Quadrada de 2, – o valor 0,7071 = Raiz Quadrade de 2/2 – (que aparece como uma distância de corda) – e imediatamente se lembrou do Triângulo Retângulo, com dois lados iguais, onde estes valôres aparecem. Intrigado com isso resolveu construir triângulos retângulos cujas hipotenusas tivessem uma sequência constituida pelos números que representam os sucessivos intervalos e viu que os catetos poderiam ser representados também na base 2 elevado […]
Séries de Fourier Seja g(t) uma função periódica de período , definida em IR e integrável, segundo Riemann, em qualquer intervalo limitado. O nosso pressuposto é averiguar se g pode ser ‘expandida’ numa série da forma . (1) Na fórmula acima, é o coeficiente correspondente à função constante , em que o fator está presente por conveniência. O termo não aparece pois . Tendo em conta que e que , a equação (1) pode ser rescrita na forma (2) com e , para cada . Para o que se segue, iremos explorar principalmente (2), contudo devemos também associar os resultados […]
BEDIENT, J., BENT, L., JONES, P., The Historical Roots of Elementary Mathematics, Prentice-Hall Inc., New Jersey, 1976 FOLLAND, Gerald B., Fourier Analysis and its applications, Brooks/Cole Publishing Company, Pacific Groove, California, 1992. HELLEGOUARCH, Yves, “Kreisleriana”, I.R.E.M de Basse-Normandie, Caen, 1985 LOI, Maurice, “Mathématiques et Art”, Hermann, Éditeurs des Sciences et des Arts, Paris, 1995 PAPADOPOULOS, Athanase, Mathematics and Music Theory: from Pythagoras to Rameau, The Mathematical Intelligencer, vol. 24, nº1, Springer-Verlag, New York, 2002 Em formato PDF ou DOC: BARBOSA, Álvaro M., “Edição Digital de Som”, Sebenta do curso de Som e Imagem da Universidade Católica Portuguesa, 1999 URL: http://www.abarbosa.org/docs/edicao_digital_som.pdf […]
No princípio era o som … Na antiguidade foram várias as civilizações que realizaram experiências no campo da acústica. A mais bem sucedida foi a civilização Grega que, por intermédio dos Pitagóricos [1], conseguiu relacionar a acústica com a aritmética. Para tal, muito terá contribuído o papel de relevo desempenhado pela música nas cerimônias gregas assim como os instrumentos por eles utilizados: instrumentos de cordas, sobretudo a cítara, ligados ao culto de Apolo; e os de sopro, sobretudo a flauta, ligados ao culto de Dionísio. Tais instrumentos terão sido bastante sugestivos aos Pitagóricos, pois tanto a cítara, com as suas […]
Influência da Matemática na Concepção de Sistemas Acústicos Na corda do cânon existe uma infinidade de sons: para cada comprimento da corda está associado um som e a comprimentos distintos correspondem sons distintos. Se atendermos a que estes sons se distinguem entre si, fundamentalmente, através das suas freqüências fundamentais, e se imaginarmos que a corda é infinita, então verificamos que existe uma bijeção entre IR0+ e o conjunto dos sons da corda – ao zero fica associado a ausência de som. Quando o músico quer compor, a primeira opção que tem que fazer é decidir quais as freqüências que quer […]
O,1,1,2,3,5,8,13,21,34,55,89,144,233… por: Prof.Luiz Netto Os números de Fibonacci plotados na espiral musical Referência: B.Vallumbrosius – Equações Vallumbrosianas (1861-1928) O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil Retornar ao Índice
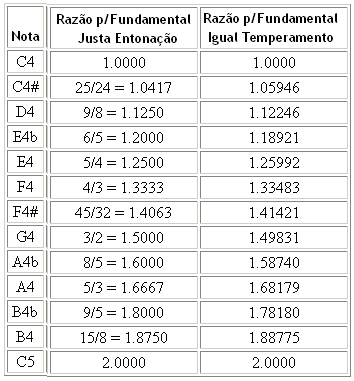
por: Prof.Luiz Netto TABELA CONSTRUIDA A PARTIR DA FREQUENCIADE DÓ DE ACÔRDO COM AS RELAÇÕES DO QUADRO ACIMA. IGUAL TEMPERAMENTO – PITAGÓRICA – JUSTA ENTONAÇÃO COMPARAÇÃO ENTRE OS INTERVALOS DE QUINTAS NAS DUAS ESCALAS – TEMPERADA E A “PURA” COMPARAÇÃO DO INTERVALO DE QUINTAS – ESCALA IGUAL TEMPERAMENTO E “PURO” O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil Retornar ao Índice
por: Prof.Luiz Netto O teclado de um acordeón – Nomes das Notas Musicais – Sustenidos – Bemóis Verifique que uma mesma nota recebe nomes diferentes – de graves para agudos: Sustenidos de Agudos para Graves: Bemois. Cada nota eleva-se ou abaixa-se de sua antecedente de um semiton, quando se percorre a escala alternadamente de notas brancas para pretas adjacentes. CONHECENDO AS TONALIDADES PELO NÚMERO DE ACIDENTES JUNTO À ARMADURA DE CLAVE Dicas de Construço das Escalas Maiores e Menores Tudo o que se precisa lembrar para fazer a construção de qualquer escala, maior ou menor, é a sua estrutura de […]
por: Prof.Luiz Netto A arquitetura das tonalidades maiores e menores obedecem uma estrutura de formação observando determinadas sequencias de Tons e Semitons como explicado logo mais abaixo com o título FORMAÇÃO. Construção das tonalidades MAIORES com sustenidos e bemóis Constroem-se as escalas com sustenidos e bemois na ordem: [sustenidos] –> Do, sol, re, la, mi si, fa#, do#, [ bemois] –> do b, sol b, re b, la b, mi b, si b, fa. FORMAÇÃO As escalas maiores obedecem em sua formação a estrutura TTS – T – TTS Tom, Tom, Semiton – TOM – Tom, Tom, Semitom, III….IV……………VII…..VIII com […]
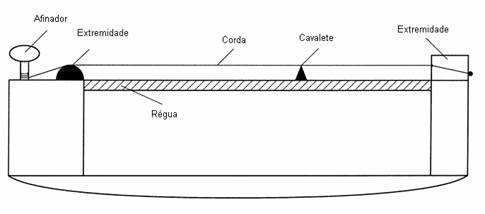
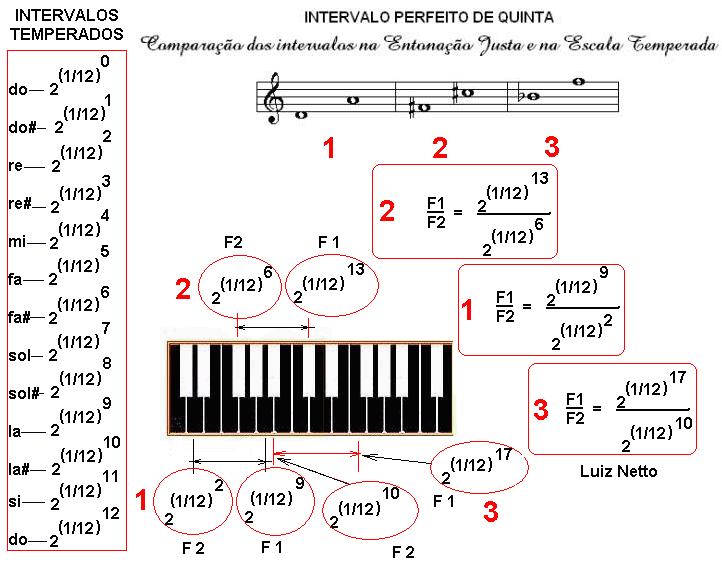
por: Prof.Luiz Netto Para compararmos os intervalos perfeitos de quinta na Entonação Justa e na Escala Temperada, onde a razão entre os quocientes de duas frequências adjacentes são sempre iguais entre si, é necessário calculá-los em unidades denominadas “Cents“, que se obtém aplicando a fórmula seguinte: Portanto, vamos aplicar essa fórmula para calcular em “Cents” o tamanho do intervalo perfeito de quinta na escala musical temperada e também para o mesmo intervalo na entonação justa e verificar a grandeza dos dois intervalos. NA ESCALA TEMPERADA NA ENTONAÇÃO JUSTA Portanto vemos que o intervalo perfeito de quinta na escala temperada é […]
por: Prof.Luiz Netto Para que servem os logaritmos? Entenda-os e descobrirá a enorme utilidade deles! Já dizia o físico italiano Galileu Galilei que a Matemática é a linguagem da Física. Uma das percepções mais agudas no campo da Matemática foi a do entendimento do que são os logaritmos, e o vislumbre de muitas aplicações de suas propriedades na descrição de muitos fenômenos da natureza. Só para citar algumas: 1)O valor do Ph das soluções, cuja acidez ou alcalinidade é medida por uma escala Logarítmica.: (Ph) –> pondus hidrogeni –> peso do hidrogênio. Ph = 7 –> (Neutro) –> significa que […]
por: Prof.Luiz Netto É curioso notar que as frequencias das notas musicais na escala musical temperada tem um comportamento de crescimento semelhante ao cálculo de juros compostos. É só considerarmos que na escala musical temperada de 12 intervalos a taxa de crescimento é de 5,94631%). Aplicando esta fórmula você pode calcular todos os valores das notas musicais da escala musical temperada de meio em meio tom, é só ir variando o expoente de zero à 12, partindo da frequencia de uma nota musical conhecida. O intervalo entre as duas notas aqui calculadas é de uma oitava porque o quociente entre […]
por: Prof.Luiz Netto Lendo o título acima alguém pode perguntar: não estaria este titulo equivocado? Bem, acho que não como logo verão neste artigo…Quando refletimos acerca dos fenômenos vibratórios e quais desses são detectados pelos seres humanos vemos que somos dotados de apenas alguns sentidos que detectam apenas alguns fenômenos que ocorrem na natureza. Miríades de outros fenômenos vibratórios permanecem desconhecidos por nossos sentidos.Certamente os sentidos que temos são aqueles mínimos necessários para manutenção, defesa e continuidade da nossa vida e que a natureza nos dotou. Tudo o mais que o homem precisa ele constrói. Se não vemos com nossos […]
por: Prof.Luiz Netto Os símbolos empregados na pauta musical para abarcar toda a tessitura dos instrumentos musicais tem variado ao longo do tempo sendo atualmente empregado os símbolos para a clave de Sol, para a clave de dó e para a clave de Fá. É curioso verificar que houve uma modificação paulatina ao longo do tempo introduzida pelos copistas de partituras, até que chegassem a essa representação nos dias de hoje, talvez na tentativa de simplificar os traços e conferir maior rapidez no desenhar. É intrigante verificar que todas elas trazem algo em comum dentro de seus traços: Algo que […]