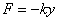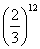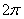      
|
|
  
|
Preparado na Escola Secundária Garcia de Orta, Portugal (ES-Garcia de Orta) Introdução Capítulo 1 – No princípio era o som … Capítulo 2 – Influência da Matemática na Concepção de Sistemas Acústicos Capítulo 3 – Som, Ondas e Números Capítulo 4 – Equação da Vibração de uma Corda Musical Anexo: Séries de Fourier Bibliografia Para fazer o download do estudo completo (formato MS Word compactado (zip) – 370 KB) clique aqui
Equação da Vibração de uma Corda Musical 4.2.1. Vibração pontual da corda Consideremos uma partícula de massa m que possui uma posição de equilíbrio y = 0. Se essa partícula for sujeita a uma força F que atue sobre ela em direção à sua posição de equilíbrio, de forma a que , ou seja, a sua magnitude seja proporcional à distância y da sua posição de equilíbrio, então essa partícula descreve um movimento harmônico simples. Este tipo de movimento é descrito por qualquer partícula de uma corda que esteja a vibrar. Assim, seja y a ordenada de uma partícula de […]
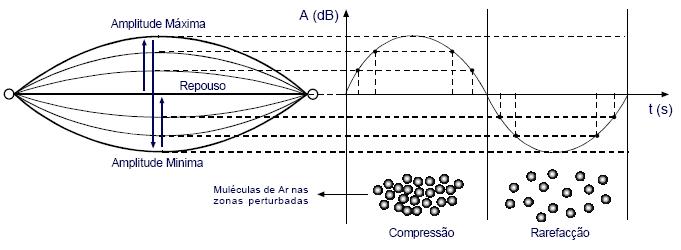
Som, Ondas e Números 3.1. O que é o som De uma forma geral, o som é uma sensação que resulta da percepção de distúrbios das moléculas de um meio num certo intervalo de tempo. Esses distúrbios, por sua vez, propagam-se no meio sob a forma de ondas. O som que ouvimos resulta dum distúrbio na atmosfera causado por um emissor, distúrbio esse que consiste em rápidas variações da pressão atmosférica que se propagam sob a forma de ondas até aos nossos ouvidos. Estas ondas provocam variações na membrana auricular, as quais vão ser transmitidas ao cérebro através de pequenos […]
Influência da Matemática na Concepção de Sistemas Acústicos Na corda do cânon existe uma infinidade de sons: para cada comprimento da corda está associado um som e a comprimentos distintos correspondem sons distintos. Se atendermos a que estes sons se distinguem entre si, fundamentalmente, através das suas freqüências fundamentais, e se imaginarmos que a corda é infinita, então verificamos que existe uma bijeção entre IR0+ e o conjunto dos sons da corda – ao zero fica associado a ausência de som. Quando o músico quer compor, a primeira opção que tem que fazer é decidir quais as freqüências que quer […]
No princípio era o som … Na antiguidade foram várias as civilizações que realizaram experiências no campo da acústica. A mais bem sucedida foi a civilização Grega que, por intermédio dos Pitagóricos [1], conseguiu relacionar a acústica com a aritmética. Para tal, muito terá contribuído o papel de relevo desempenhado pela música nas cerimônias gregas assim como os instrumentos por eles utilizados: instrumentos de cordas, sobretudo a cítara, ligados ao culto de Apolo; e os de sopro, sobretudo a flauta, ligados ao culto de Dionísio. Tais instrumentos terão sido bastante sugestivos aos Pitagóricos, pois tanto a cítara, com as suas […]
BEDIENT, J., BENT, L., JONES, P., The Historical Roots of Elementary Mathematics, Prentice-Hall Inc., New Jersey, 1976 FOLLAND, Gerald B., Fourier Analysis and its applications, Brooks/Cole Publishing Company, Pacific Groove, California, 1992. HELLEGOUARCH, Yves, “Kreisleriana”, I.R.E.M de Basse-Normandie, Caen, 1985 LOI, Maurice, “Mathématiques et Art”, Hermann, Éditeurs des Sciences et des Arts, Paris, 1995 PAPADOPOULOS, Athanase, Mathematics and Music Theory: from Pythagoras to Rameau, The Mathematical Intelligencer, vol. 24, nº1, Springer-Verlag, New York, 2002 Em formato PDF ou DOC: BARBOSA, Álvaro M., “Edição Digital de Som”, Sebenta do curso de Som e Imagem da Universidade Católica Portuguesa, 1999 URL: http://www.abarbosa.org/docs/edicao_digital_som.pdf […]
Séries de Fourier Seja g(t) uma função periódica de período , definida em IR e integrável, segundo Riemann, em qualquer intervalo limitado. O nosso pressuposto é averiguar se g pode ser ‘expandida’ numa série da forma . (1) Na fórmula acima, é o coeficiente correspondente à função constante , em que o fator está presente por conveniência. O termo não aparece pois . Tendo em conta que e que , a equação (1) pode ser rescrita na forma (2) com e , para cada . Para o que se segue, iremos explorar principalmente (2), contudo devemos também associar os resultados […]
por: Prof.Luiz Netto O sábio matemático Bernardus Vallumbrosius, certamente que ao contemplar os valores constituintes da Escala Musical Temperada, notou algumas valôres que lhe pareceram bem familiares como 1,4142 = Raiz Quadrada de 2, – o valor 0,7071 = Raiz Quadrade de 2/2 – (que aparece como uma distância de corda) – e imediatamente se lembrou do Triângulo Retângulo, com dois lados iguais, onde estes valôres aparecem. Intrigado com isso resolveu construir triângulos retângulos cujas hipotenusas tivessem uma sequência constituida pelos números que representam os sucessivos intervalos e viu que os catetos poderiam ser representados também na base 2 elevado […]
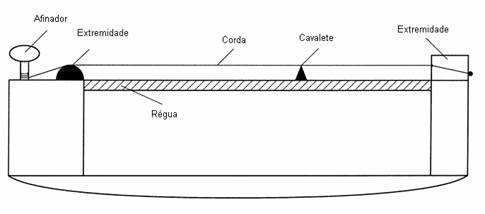
por: Prof.Luiz Netto Parte 1 (*) Antes que possamos chegar aos cálculos para dimensionamento das distâncias dos trastes nos instrumentos musicais de corda, vejamos algumas considerações matemáticas que são indispensáveis sejam feitas para o entendimento de como proceder esse dimensionamento. O nível de conhecimento de matemática exigido para este propósito é que se consiga operar com logarítimos e exponenciais. Se você tem alguma dificuldade para entender a matemática que está por trás deste estudo, não se assuste, aqui há também Tabelas Práticas para consulta. A faixa de audio detetada pelo ser humano está em torno de 10 oitavas, desde 20 […]
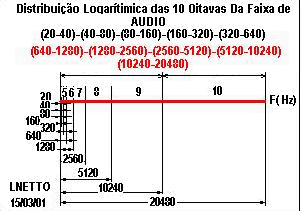
por: Prof.Luiz Netto Quando Landell de Moura construiu o seu TRANSMISSOR DE ONDAS, sabia de suas qualidades e também das limitações técnicas do aparelho e deixou-as muito claramente explicitadas e por isso pediu apoio para continuar os seus estudos que afinal acabaram por não vir. Deixou claro que o aparelho perderia muitos harmônicos contidos nas palavras emitidas, justamente porque os Harmônicos variam em frequência e em amplitude também. Naturalmente ele teria que fixar uma distância entre o ponto de contacto elétrico e o diafragma captador da voz para fechar o circuito do primário da Bobina de Ruhmkorff e por isso […]
por: Prof.Luiz Netto Construção das escalas menores com sustenidos e bemóis FORMAÇÃO das ESCALAS MENORES As escalas menores obedecem em sua formação a estrutura TST – TST – T Tom, Semiton, Tom – Tom, Semiton, Tom – Tom I…………….II……..III………………IV………………V………………VI……VII………………VIII com os semitons colocados entre o II e III graus e VI e VII graus. As escalas menores formam-se a partir do VI Grau da Escala de Tonalidade Maior Assim, a relativa menor de do maior, começará em la. Do, re, mi, fa, sol, LA. As relativas menores tem a mesma armadura de clave que suas correspondentes maiores. Assim, vamos construir […]
por: Prof.Luiz Netto A arquitetura das tonalidades maiores e menores obedecem uma estrutura de formação observando determinadas sequencias de Tons e Semitons como explicado logo mais abaixo com o título FORMAÇÃO. Construção das tonalidades MAIORES com sustenidos e bemóis Constroem-se as escalas com sustenidos e bemois na ordem: [sustenidos] –> Do, sol, re, la, mi si, fa#, do#, [ bemois] –> do b, sol b, re b, la b, mi b, si b, fa. FORMAÇÃO As escalas maiores obedecem em sua formação a estrutura TTS – T – TTS Tom, Tom, Semiton – TOM – Tom, Tom, Semitom, III….IV……………VII…..VIII com […]
por: Prof.Luiz Netto O teclado de um acordeón – Nomes das Notas Musicais – Sustenidos – Bemóis Verifique que uma mesma nota recebe nomes diferentes – de graves para agudos: Sustenidos de Agudos para Graves: Bemois. Cada nota eleva-se ou abaixa-se de sua antecedente de um semiton, quando se percorre a escala alternadamente de notas brancas para pretas adjacentes. CONHECENDO AS TONALIDADES PELO NÚMERO DE ACIDENTES JUNTO À ARMADURA DE CLAVE Dicas de Construço das Escalas Maiores e Menores Tudo o que se precisa lembrar para fazer a construção de qualquer escala, maior ou menor, é a sua estrutura de […]
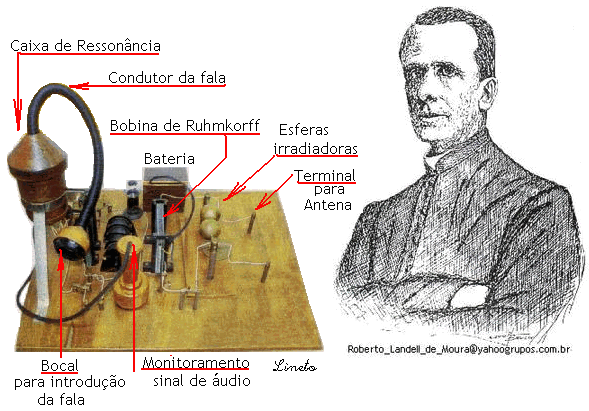
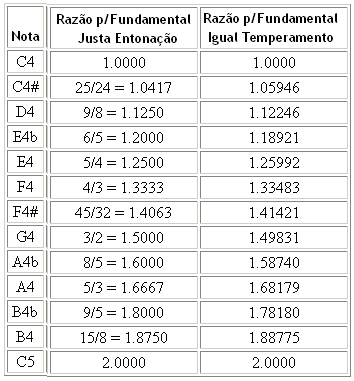
por: Prof.Luiz Netto TABELA CONSTRUIDA A PARTIR DA FREQUENCIADE DÓ DE ACÔRDO COM AS RELAÇÕES DO QUADRO ACIMA. IGUAL TEMPERAMENTO – PITAGÓRICA – JUSTA ENTONAÇÃO COMPARAÇÃO ENTRE OS INTERVALOS DE QUINTAS NAS DUAS ESCALAS – TEMPERADA E A “PURA” COMPARAÇÃO DO INTERVALO DE QUINTAS – ESCALA IGUAL TEMPERAMENTO E “PURO” O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil Retornar ao Índice
O,1,1,2,3,5,8,13,21,34,55,89,144,233… por: Prof.Luiz Netto Os números de Fibonacci plotados na espiral musical Referência: B.Vallumbrosius – Equações Vallumbrosianas (1861-1928) O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil Retornar ao Índice
Se desejar receber as novidades, artigos e atualizações deste site, digite seu endereço de e-mail no campo abaixo:
Não deixe de responder ao e-mail de confirmação!
Visite nosso canal: 