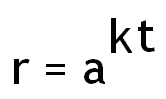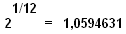por: Prof.Luiz Netto r = a^(kt) Além da representação da escala musical temperada com seus vetores frequencia representados no espaço bidimensional, podemos fazer esta representação também no espaço tridimensional. Devo dizer que nunca vi isto deste modo, apenas proponho esta maneira de representá-la, como o fiz na representação polar em duas dimensões. Podemos imaginar os vetores girando em torno de um cilindro cujo raio da base tem o valor (1.0594631)^(1.9098593 t) para t = zero, com origens no centro do cilindro e cujas pontas percorram as paredes do cilindro subindo exponencialmente, de acordo com a equação (1.0594631)^(1.9098593 t). A equação […]
Artigos do Prof. Ángel Franco García (Universidad del País Vasco – España)(Atenção: as referências abaixo direcionam para páginas externas ao Música Sacra e Adoração, as quais estão no idioma Espanhol. Sugerimos não utilizar tradutores automáticos para ler o conteúdo, pois as excelentes aplicações com exemplos poderão deixar de funcionar.) Acústica 1 – Ondas Estacionarias en Tubos Abiertos o Cerrados 2 – Medida de la Velocidad de las Ondas Longitudinales 3 – Velocidad de Propagación del Sonido en un Gas 4 – El Resonador de Helmholtz 5 – Análisis de Fourier 6 – Efecto Doppler Acústico 7 – Efecto Doppler Acústico […]
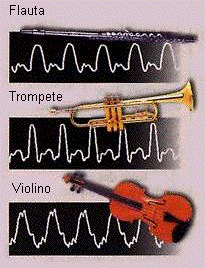
por: Naylor Oliveira Características sonoras A ciência pode hoje apontar certas características físicas de um som musical que o distingue de sons que são apenas ruídos. Utilizando instrumentos que transcrevem as ondas sonoras em imagens visuais (tais como o “osciloscópio”), os cientistas aprenderam que a maioria dos sons musicais formam estruturas definidas por ondas e descritas por funções matemáticas (chamadas de “função seno” ou “senóide”), e que cada instrumento produz uma modalidade matemática diferente. O som é medido fisicamente por três grandezas; a intensidade, a freqüência e o timbre. Intensidade refere-se à amplitude das oscilações da pressão do ar. Freqüência […]
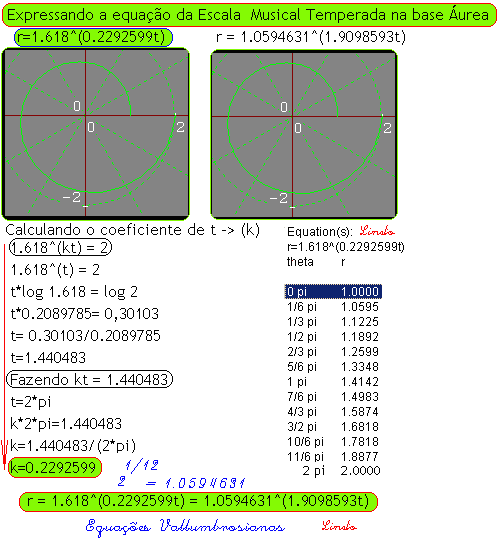
por: Prof.Luiz Netto A título de exercício fazemos aqui o cálculo de como expressar a equação da escala musical temperada cuja base é a raiz décima segunda de dois, que é igual a 1.0594631, na base áurea que é igual a 1.618. O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil Retornar ao Índice
por: Prof.Luiz Netto Graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil Distâncias dos Trastes nos Instrumentos Musicais de Cordas ou Comprimentos das Cordas nos Instrumentos Musicais Observe como varia o comprimento das cordas; é uma variação exponencial e não linear. Vimos em artigo anterior que o matemático Bernardus Vallumbrosius observou que os intervalos musicais da escala musical temperada podiam ser compostos como linhas de um triângulo retângulo. Assim também é possivel compor a representação dos comprimentos das cordas vibrantes que geram os sons da escala musical temperada, ou o que […]
por: Prof.Luiz Netto Dadas duas frequências f1 e f2 o intervalo entre elas é dado pelo quociente f2/f1. Isto posto podemos escrever que: Exemplo de intervalo de uma oitava, de La2 à La3 ou escrevendo em forma exponencial para um intervalo genérico qualquer, temos que, Aplicando logarítmos para resolver a equação, vem que x.log f1 = log f2 Donde vem que: Por outro lado, como já vimos anteriormente, o intervalo de um cent vale Podemos relacionar 1 e 2 Assim para convertermos qualquer intervalo musical em Cents, utilizamos a formula final abaixo Assim, o intervalo de 1 oitava, quantos Cents […]
por: Prof.Luiz Netto Unidades de Medidas O Cent – O Savart O cent e o savart são unidades de medidas que permitem medir intervalos sonoros bem pequenos. A percepção da menor variação em frequência detectada pelo ouvido varia ao longo da faixa de áudio. O ouvido é bastante sensível aos sons graves e tem sua sensibilidade máxima entre 3,5 e 4.0 Khz, muito próximo da primeira zona de ressonância que ocorre no ouvido externo. A segunda zona de ressonância ocorre próximo aos 13 Khz. A capacidade de distinção do ouvido em relação à menor variação de frequência, depende da frequência […]
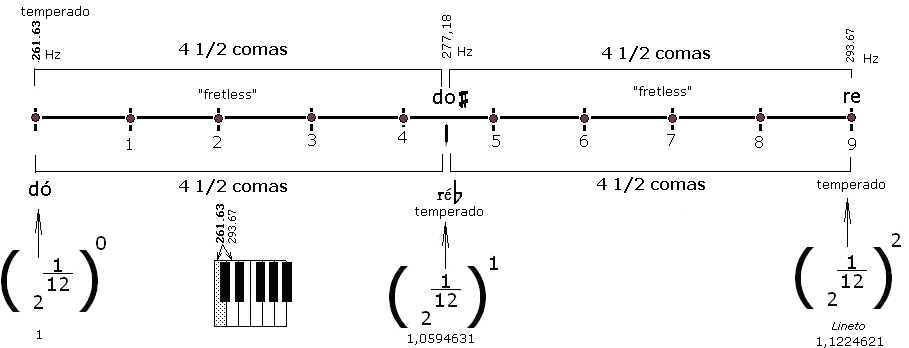
por: Prof.Luiz Netto Pontos comuns com a escala temperada – Cálculos No sistema temperado os intervalos são iguais. Coma é um intervalo musical. O intervalo de 1 tom compreende os intervalos de 9 comas. Portanto no sistema igualmente temperado ao intervalo de 1/2 tom corresponde ao intervalo de 4 e 1/2 comas. O intervalo coma é obtido dividindo o “espaço” de um tom em 9 intervalos. Portanto as notas musicais obtidas nestes intervalos só são possiveis de serem executadas nos instrumentos “fretless” ou seja nos instrumentos que não tem trastes pois nestes os intervalos são de meio em meio tom. […]
por: Prof.Luiz Netto Quando se estuda o dimensionamento das distâncias entre os trastes dos instrumentos musicais de cordas, calcula-se matemáticamente onde deve ficar os trastes e parece que está tudo resolvido, é só pontear as cordas em determinadas posições e ter-se-à o som matematicamentete calculado, com a frequência determinada. Só que as coisas não acontecem exatamente assim. E porque? Por uma razão muito simples de se entender. Olhando a para a figura situada logo mais abaixo você vai entender o porque. Ao se aplicar o dedo sobre a corda exerce-se sobre esta uma sobretensão. Ora, o instrumento havia sido afinado […]
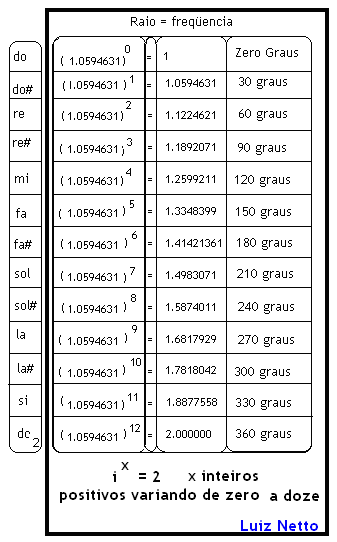
por: Prof.Luiz Netto Na tabela acima vemos que as notas musicais podem ser representadas em notação polar, associando ao valor de cada nota um ângulo.Como temos em uma circunferência 360 graus ou 2 pi radianos, e temos na escala musical temperada doze intervalos, a cada intervalo de meio tom (100 cents) – corresponderá 30 graus, ou pi/6 radianos. O problema que nos propomos a resolver é dado um desses valores, calcular o ângulo que lhe corresponde: Seja o problema: Sabemos que o valor da nota é igual a 1.4983071 que corresponde à nota Sol, qual é o ângulo que está […]
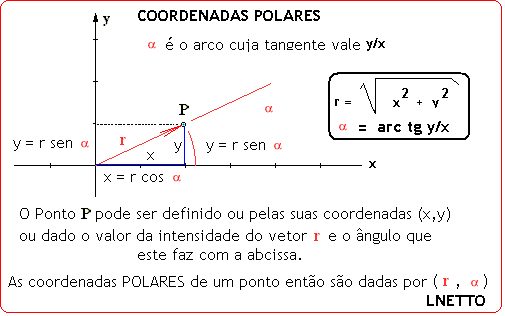
por: Prof.Luiz Netto Assim se temos (r, alfa), imediatamente podemos transformar as coordenadas desse ponto dada em coordenadas polares para coordenadas cartesianas: Seja r = 5 e alfa = 25 graus, então: y = r.sen(alfa)-> y = 5.sen 25 -> y = 5.0,4226182 -> y = 2,113091 x = r cos (alfa) -> 5.cos 25 -> x = 5.0,9063077 -> x = 4,5315385 ou fazendo o inverso, se temos as coordenadas x e y e queresmos as coordenadas polares: Seja: x = 4,5315385 y = 2,113091 e queremos expressar as coordenadas cartesianas desse ponto em coordenadas polares: Qual é o […]