por: Carlos Alexandre Wuensche de Souza
1 – Introdução
Quando falamos de som e música, raramente pensamos em física e na análise científica necessária para entender a propagação do som e suas nuanças, nas propriedades físicas do som e nos detalhes ligados ao processo que antecede a apreciação da arte musical. Esta monografia apresenta a parte da Física ligada ao processo da produção e análise dos sons, em particular os musicais: a Acústica.
A ligação da música com a ciência – em outras palavras, a associação da estética musical à teoria dos números – remonta à Escola Pitagórica, no século VI a.C. O ponto de partida era a relação entre os comprimentos das cordas de uma lira e as notas musicais e a percepção que cordas mais curtas emitiam sons mais agudos .A partir daí foi desenvolvida uma teoria completa, relacionando comprimentos de cordas, escalas, intervalos, notas, números inteiros e frações. Em particular, a associação de uma fração a um dado intervalo musical mostrou-se um dos princípios mais fecundos da acústica e em cima dele montou-se praticamente toda a teoria da música ocidental (ver, por exemplo, a referência 4). A relação entre a Física e a Música começou a aparecer de maneira mais sistemática junto com a criação da teoria ondulatória, estabelecida nos sécs. XVII e XVIII, e sedimentou-se quando Jean Batiste Fourier criou, no início do séc. XIX, uma ferramenta matemática para estudar fenômenos periódicos, hoje conhecida como análise de Fourier. Falaremos superficialmente sobre a análise de Fourier em diversas partes dessa monografia.
Trataremos também da percepção do som a partir das suas propriedades físicas, que nos permitem ouvir o som sem, necessariamente, estar na frente da fonte sonora. Como toda onda, o som sofre reflexão, é absorvido pelo meio em que se propaga, atenuado pelo atrito com as moléculas do meio e transmitido de um meio a outro. Usando essas ferramentas vamos então discutir os detalhes da produção do som nos diversos instrumentos musicais e entender o porquê das peculiaridades sonoras de cada um deles e porque um som musical é diferente de um som qualquer produzido na natureza.
2 – Produção do Som
O som é produzido ao criarmos algum tipo de mecanismo que altere a pressão do ar em nossa volta. Na verdade, para a produção do som, é mais importante a velocidade com que a pressão varia (o "gradiente da pressão", no jargão dos físicos) do que o seu valor absoluto. Por essa razão é que um balão cheio de ar não faz praticamente nenhum barulho ao deixarmos o ar sair de dentro dele naturalmente. Por outro lado, se o balão estourar (e o ar sair todo de uma vez), existe uma variação enorme da pressão e um ruído alto é produzido. Podemos então dizer que o som é produzido ao colocarmos uma quantidade (massa) de ar em movimento. É a variação da pressão sobre a massa de ar que causa os diferentes sons, dentre eles os que são combinados para criar a música. A vibração de determinados materiais é transmitida às moléculas de ar sob a forma de ondas sonoras. Percebemos o som porque as ondas no ar, causadas pela variação de pressão, chegam aos nossos ouvidos e fazem o tímpano vibrar. As vibrações são transformadas em impulsos nervosos, levadas até o cérebro e lá codificadas. Quando essa vibração ocorre de uma maneira repetitiva, rítmica, ouvimos um tom, com uma altura igual à sua freqüência. Um cantor cuja voz é classificada como baixo possui uma faixa de alturas situada, normalmente, entre 80 e 300 Hz. Uma cantora classificada como soprano possui a faixa de alturas entre 300 e 1100 Hz. Os instrumentos musicais podem produzir tons dentro de um intervalo muito maior do que o da voz humana. O ouvido humano, porém só percebe sons cuja freqüência se limita ao intervalo entre 20 e 20000 Hz. Vamos discutir os conceitos de tom, altura e freqüência (onde definiremos o que é um Hertz, ou Hz) na próxima seção.
A analogia entre a compressão e a rarefação do ar ao transmitir as ondas sonoras pode ser vista ao brincarmos com uma mola, facilmente encontrada em lojas de brinquedos infantis. O nosso problema agora é quantificar a produção do som a partir desta variação de pressão. Uma maneira interessante de se fazer isso é mostrar como, num tubo tampado, a modificação da pressão interna que acontece quando ele é destampado, produz um som característico. Esse som pode ser observado num osciloscópio e registrado no computador, caso ele possua uma placa de som e um microfone. Qualquer dos programas de computador que vem junto com a placa de som é capaz de gravar e reproduzir esse som.
Uma nota musical é um som cuja freqüência de vibração encontra-se dentro do intervalo perceptível pelo ouvido humano e a música é a combinação, sob as mais diversas formas, de uma seqüência de notas musicais em diferentes intervalos. Um intervalo é uma relação entre as freqüências de duas notas musicais. Entretanto, uma mesma nota emitida por diferentes fontes (ou instrumentos musicais) pode ter a mesma freqüência e ainda assim soar de maneira diferente para quem ouve. Atualmente os princípios da Acústica e a teoria da propagação das ondas são bastante bem conhecidos e pode-se descrever com precisão todas as peculiaridades e características associadas a fenômenos sonoros em geral. A análise de Fourier afirma que qualquer onda ou, mais genericamente, qualquer movimento periódico, pode ser decomposta em uma combinação de ondas primitivas, todas elas com a forma de uma senóide. Vamos agora entender essa descrição matemática um pouco mais detalhadamente.
3 – Descrevendo Cientificamente um Som
A forma de onda vista abaixo possui a forma da função matemática conhecida como função seno ou senóide. Podemos descrever completamente essa função em termos da sua amplitude, comprimento de onda e freqüência.
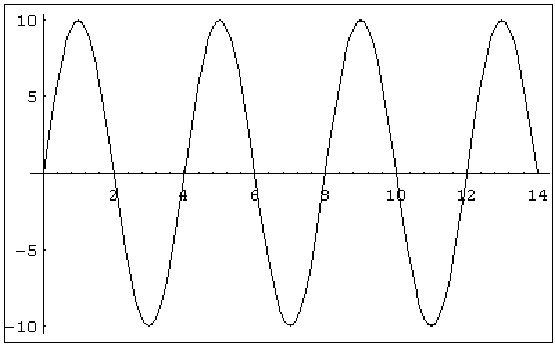
Figura 1 – Uma função seno, com amplitude variando de 10 a -10 e comprimento de onda igual a 4 cm
A Figura 1 vai nos ajudar a definir praticamente todas as grandezas de que necessitamos para descrever os sons durante o resto do texto. O comprimento de onda é a grandeza física que define o "tamanho do ciclo", ou seja, qual a distância percorrida por um ciclo de onda até que ele volte a se repetir. Na nossa figura, um comprimento de onda é a distância, no eixo horizontal (X), de 0 a 4, 4 a 8, 8 a 12 e assim por diante. Assim, dizemos que a nossa onda tem 4 unidades de comprimento de onda (que pode ser expresso em metros, centímetros ou qualquer outra unidade que você desejar). A amplitude é o afastamento da forma de onda da origem, na direção vertical Assim, a amplitude máxima na Figura 1 é de 10 unidades, quer para cima, quer para baixo. A freqüência descreve o número de vibrações por unidade de tempo, ou seja, quantos ciclos completos a onda percorre em uma unidade de tempo, que pode ser o segundo, o minuto ou qualquer outra unidade que você achar conveniente. A unidade que usaremos para descrever as freqüências é o Hertz (Hz). 1 Hz corresponde a um ciclo de vibração por segundo. Por exemplo, quando colocamos um diapasão na forma de garfo em vibração, suas hastes vibrarão a uma freqüência de 440 Hz, ou 440 ciclos por segundo, correspondentes à nota musical Lá4. Essa nota pode ser perfeitamente descrita pela sua freqüência (440 Hz), comprimento de onda (0,77 m) e uma amplitude que vai depender da energia utilizada para colocá-lo em vibração e que descreve a intensidade da variação da pressão do ar.
Outra característica importante de uma onda, normalmente mencionada nos livros de Física de nível médio, é que ela transporta energia sem transportar matéria. Isso pode ser observado quando jogamos uma pedra numa piscina com água parada. Não há transporte das moléculas de água, mas observamos uma "perturbação" se propagando do ponto onde jogamos a pedra para todos os pontos na borda da piscina. Podemos ver que ela transporta energia, caso haja uma folha na superfície da água. Quando a perturbação passar pela folha, ela vai entrar em movimento (na direção vertical, atingindo o pico da onda, e depois descendo passando pelo "vale" da onda), voltando ao repouso depois da passagem. Essa característica, aplicada ao caso da produção de sons, faz com que as ondas sonoras passando próximas ao ouvido coloquem o tímpano para se movimentar (oscilar), devido ao movimento das moléculas de ar.
4 – Freqüências Naturais, Harmônicos e Sobretons
Qualquer objeto ou corpo sólido, e mesmo as pequenas moléculas que formam os objetos macroscópicos, possuem uma certa vibração natural, uma "freqüência característica". Isso ocorre porque os átomos possuem uma energia de agitação, uma propriedade explicada pela mecânica quântica e pela termodinâmica, que está associada à sua temperatura. Os físicos chamam essa energia de energia térmica. A combinação das freqüências de todos os átomos cria um "padrão de vibração" que caracteriza os corpos, sejam eles musicais ou não.
Entretanto, as freqüências ligadas à música são criadas por um mecanismo diferente. É necessário "excitar", estimular externamente um corpo, para que ele emita um som. Em outras palavras, é necessário que se aplique uma força a esse corpo para que o elemento vibrante (que transmitirá a energia às moléculas de ar) seja colocado em movimento. Se movimentarmos um diapasão de garfo (batendo com ele na borda de uma mesa, por exemplo), o movimento das suas hastes empurra e comprime o ar com a mesma freqüência com que elas vibram. No caso do diapasão típico, a freqüência natural de vibração é de 440 ciclos por segundo, ou 440 Hz. Ela depende, como você deve estar imaginando, do tipo de material com o qual o diapasão é construído: densidade, rigidez, a constituição molecular, forma e uma enorme variedade de fatores. Podemos exemplificar essa diferença se compararmos dois diapasões, feitos do mesmo material, com a mesma forma, mas modificando a separação entre as hastes. Eles vibrarão com freqüências diferentes: o que tiver menor separação entre as hastes vibrará mais rapidamente. Da mesma forma, se escolhermos outros dois com o mesmo material, forma e separação entre as hastes, mas com uma pequena diferença no comprimento das hastes, o que tem hastes mais longas vibrará mais lentamente.
Um outro exemplo de padrões de vibração característicos pode ser observado quando damos uma pancada leve no tampo de um violão ou na caixa de ressonância de um piano. É notável a diferença de som produzido, causado pela combinação dos fatores que mencionamos acima.
A combinação desse padrão de vibração (a soma das diversas freqüências individuais) pode ser representada, genericamente, na forma descrita abaixo:
| SOM = C1 + C2 + C3+ C4 + C5 + C6 + …, |
em que a contribuição de cada termo Cn corresponde a uma determinada freqüência, múltipla da freqüência do termo C1. Chamamos essa série de "série harmônica" e cada termo da série é chamado de harmônico. Assim, o primeiro termo é o harmônico de ordem 0 (ou fundamental); o segundo, harmônico de primeira ordem, e assim sucessivamente.
|
C1 |
C2 |
C3 |
SOM |
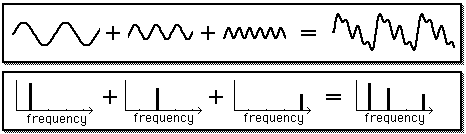
Figura 2 – Combinação dos diferente comprimentos de onda e frequências individuais para formar um padrão sonoro.
E os sobretons? Os sobretons são uma outra nomenclatura para nos referirmos aos termos da serie harmônica. Podemos defini-lo como uma componente de um som complexo que tem uma altura maior (ou que possui uma freqüência mais alta) que a componente fundamental daquele som. Assim, o termo fundamental é o TOM (fundamental) e os termos seguintes são os SOBRETONS (ou tons de freqüência superior ou componentes secundárias). O exemplo mais fácil de ser entendido pode ser visto ao decompormos uma nota musical; por exemplo, o Lá fundamental do piano (Lá4) vibra a uma freqüência de 440 Hz. O segundo harmônico (primeiro sobretom) vibrará em 880 Hz, o terceiro (segundo sobretom) em 1760 Hz. As noções de tom, sobretom e harmônico serão extremamente úteis quando discutirmos a análise de um som musical.
5- Criando uma Nota Musical
A música ocidental caracteriza-se por um conjunto definido de freqüências (que são representados pelas doze notas musicais, em diferentes alturas); os instrumentos musicais devem ser capazes de produzir essas freqüências e amortecer as outras, que estão contidas no intervalo em que o ouvido humano é sensível. Sistemas vibrantes ressonantes são excitados por essas freqüências, que correspondem às freqüências de ressonância do sistema (por sistema podemos entender qualquer instrumento capaz de produzir sons, não necessariamente musicais). A produção do som está associada à transferência de energia por um elemento excitador (por exemplo o arco de um violino) para o veículo produtor do som, seguida da colocação do ar em movimento e da sustentação da intensidade em níveis aceitáveis para que o som possa ser aproveitado em termos musicais. Podemos descrever um caso particular do violino, onde o arco é movimentado, provocando a vibração das cordas através do atrito entre a crina do arco e a superfície metálica da corda. Essa energia é transferida para o tampo através da ponte, colocando então o tampo e o ar contido dentro dele em vibração. A saída do ar se dá pelos "f" situados nos dois lados do tampo.
A seqüência de transferência pode ser imaginada da seguinte forma: um vibrador primário, unidimensional (a corda), transfere a energia para um vibrador secundário, bidimensional (o tampo), que excita a massa de ar no interior da caixa acústica do instrumento.
Os instrumentos de sopro possuem um sistema em que a própria coluna de ar é colocada em vibração, e a variação da força que empurra a coluna de ar (o "sopro") é capaz de produzir o som que é transferido para fora da saída de ar do instrumento e pela vibração de seu próprio corpo. O conjunto de chaves diversas modificam o tamanho da coluna de ar, fazendo assim com que diferentes freqüências sejam produzidas, da mesma forma que os dedos, apertando as cordas do violino, modificam o comprimento da corda vibrante. A boca desempenha o papel de agente excitador (da mesma forma que os dedos, a palheta ou o arco no caso dos instrumentos de corda) e o elemento gerador da vibração é a própria coluna de ar.
Já os instrumentos de percussão são os mais simples, porque a própria membrana vibrante (couro ou materiais rígidos) transfere energia diretamente para o ar. Não é por outra razão que os instrumentos de percussão são os mais eficientes produtores de som. Novamente, o elemento excitador é a mão humana (ou algo empunhado pelo corpo humano) e a transferência ocorre diretamente do sistema bidimensional (a membrana vibrante) para o ar, sem nenhum tipo de interferência, exceto a própria mão humana que pode ser usada para abafar ou ressaltar algum tipo de som (é o caso da posição da mão de quem toca pandeiro ou tamborim).
Cada tipo de instrumento tem uma espécie de "assinatura", um conjunto de características sonoras associado que, embora possa parecer subjetivo, possui uma descrição matemática extremamente precisa. Na seção anterior comentamos que o som pode ser representado pela soma de diversas ondas individuais, que chamamos de componentes de Fourier. O que diferencia um instrumento de outro são as amplitudes e o tempo de duração de cada um dos harmônicos presentes no som resultante e o resultado acústico da combinação das duas propriedades tem o nome de timbre.
6 – Propriedades Físicas do Som
A percepção sonora de um ouvinte numa sala de concerto ou em um ambiente fechado não é só resultado da forma como o som é produzido no instrumento. Uma série de fenômenos explicados pela teoria ondulatória influencia essa percepção de modo muitas vezes dramático. Por exemplo, podemos citar as tentativas muitas vezes frustradas de se fazer shows de bandas de rock em locais fechados como ginásios esportivos. Todos nós percebemos a interferência e uma espécie de "eco" com o qual os engenheiros de som sempre têm problemas. A percepção do som da banda é uma se estamos de frente para o palco, diferente se nos encontramos fora do "eixo" das caixas de som e ainda outro se estivermos do lado de fora do ginásio. Em todos esses casos, estaremos ouvindo a mesma banda, tocando a mesma música, mas algumas das propriedades ligadas à propagação das ondas afetam essa percepção. Os principais efeitos com os quais os engenheiros de som e músicos tem que lidar são:
- a difração,
- a reflexão,
- a interferência,
- os efeitos de transmissão, absorção e dispersão das ondas.
A difração é a mudança na direção da propagação da onda devido à passagem do som por um obstáculo qualquer. Isso permite que possamos ouvir o rádio num local da casa diferente de onde o rádio se encontra. É notável a relação entre o comprimento de onda, as dimensões do obstáculo e a difração. Quanto maior a razão entre os dois primeiros, maior é a difração.
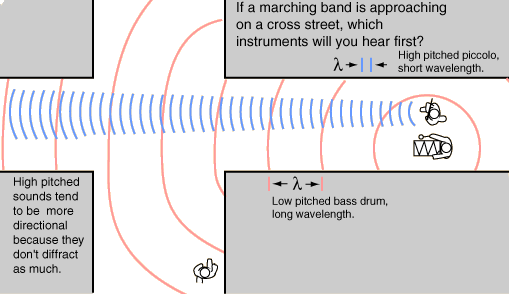
A reflexão, observada quando existe o encontro de uma onda com uma superfície rígida, mantém as características da onda incidente e ocorre sempre que as dimensões da superfície rígida forem muito maiores do que o comprimento de onda. Um exemplo interessante de reflexão sonora é o eco, observado sempre que a onda incidente possui intensidade suficiente e permite um atraso suficiente para que a onda refletida seja percebida distintamente.
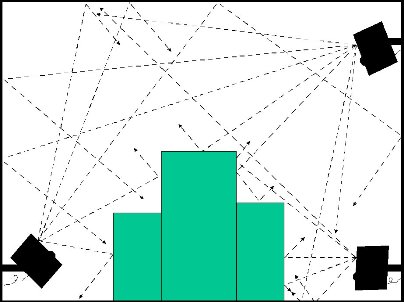
A interferência é causada pela combinação (em fase ou fora de fase) de duas ou mais ondas, fazendo com que a onda resultante seja mais intensa que as ondas originais, ou que se cancelem, no caso de uma interferência destrutiva. A interferência positiva, quando realimentada de forma adequada (aumentando a amplitude em fase, a cada ciclo) dá origem ao fenômeno da RESSONÂNCIA.
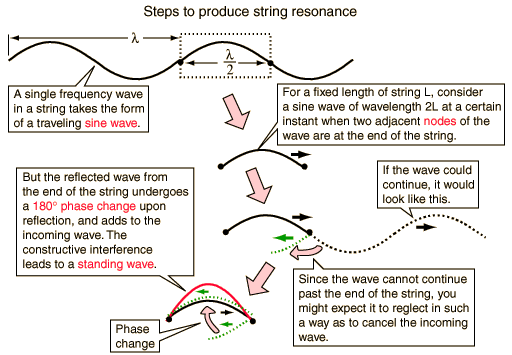
A absorção e a transmissão, de uma certa forma modificam as características da onda incidente. A absorção ocorre quando uma onda atinge um obstáculo qualquer e deposita parte de sua energia sonora ali, sendo refletida, transmitida ou refratada com uma intensidade menor. A parcela de energia depositada normalmente é transformada em calor. A transmissão acontece em praticamente todos os refletores ou absorvedores de som, causando uma propagação da onda na superfície rígida que causou uma reflexão, por exemplo. Tecnicamente, os três últimos fenômenos mencionados ocorrem sempre que uma onda atinge uma superfície rígida.
7 – Como Percebemos a Mistura de Sons
Nosso ouvido é uma espécie de "sonar", um instrumento que gera uma corrente elétrica ao ser estimulado por qualquer tipo de onda sonora. Mas por que reagimos diferentemente a diferentes tipos de sons? A resposta está ligada à freqüência com que o tímpano é movimentado pela onda que entre no canal auditivo. Como mencionamos anteriormente, ele não reage somente à nota pura (fundamental), mas também a todas as outras freqüências superiores que constituem aquele som. É interessante perceber as diferentes componentes de um mesmo som e um sintetizador capaz de produzir notas puras pode ser um valioso instrumento de auxílio no estudo desse problema.
Por exemplo, vamos tocar uma nota pura no sintetizador e vamos considerar essa nota como sendo a fundamental de freqüência f. Mantendo esse som, vamos tocar um outro simultaneamente, de freqüência 2f. Com um pouco de prática, podemos distinguir entre o primeiro e o segundo, mais alto, mesmo com ambos soando ao mesmo tempo. Mas será muito difícil diferenciar os dois se começarmos a tocar os dois ao mesmo tempo. O efeito é ainda mais impressionante se fizermos isso com as cinco primeiras componentes de uma série harmônica (f, 2f, 3f, 4f, 5f). Tocamos em seqüência as 5 freqüências e um ouvido bem treinado é, por vezes, capaz, de "separar" as freqüências individuais. Se pararmos de tocar e iniciarmos novamente, só que desta vez tocando as cinco simultaneamente, passaremos então a ouvir um som complexo e será muito mais complicado "convencer" o nosso cérebro a ouvir somente uma das componentes daquele som.
A mesma ideia pode ser tentada com diferentes harmônicos (por exemplo, f + 3f + 5f, ou 4f + 5f + 6f); o resultado será bastante diferente em qualidade, mas será sempre mais simples separar os sons se eles forem iniciados em seqüência.
Variações em amplitude também permitem um resultado sonoro interessantíssimo na qualidade do som resultante.
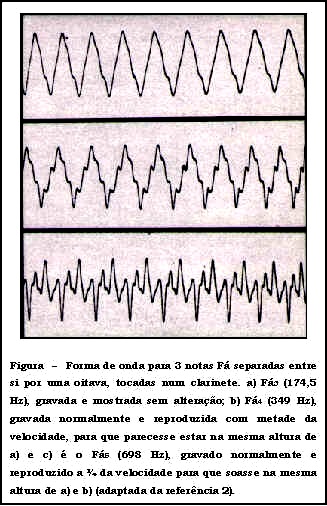
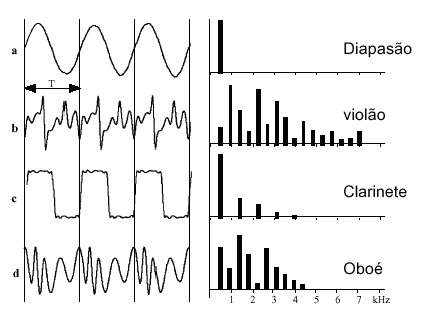
O osciloscópio pode mostrar a diferença nas combinações de som de diferentes instrumentos (mais simples de ser percebido) e mesmo em diferentes notas tocadas por um mesmo instrumento. Por exemplo, vemos na Figura 2 a notas Fá3, Fá4 e Fá5 tocadas num clarinete e ajustadas em velocidade e freqüência para que todas pareçam estar na mesma altura. Elas foram gravadas e colocadas em paralelo e a diferença é notável, mesmo depois do ajuste feito.
8 – A Análise dos Sons Musicais
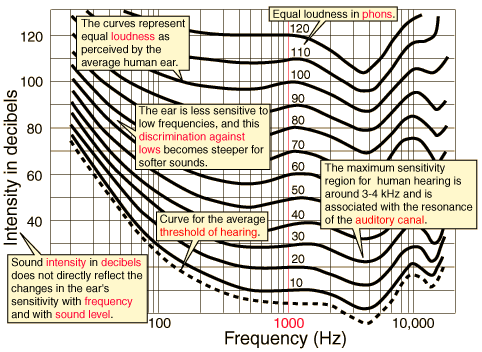
O ouvido humano médio é capaz de distinguir cerca de 1400 freqüências discretas, variando entre cerca de 20 Hz e 20000 Hz. Sons fora deste intervalo não são percebidos, ou porque não possuem energia suficiente para excitar o tímpano, ou porque a freqüência é tão alta que o tímpano não consegue perceber – é como se ele não tivesse tempo para se preparar para mandar os sinais para o cérebro, já que eles chegam muito mais rápido do que o tempo em que o tímpano é capaz de identificar uma vibração. Entretanto, quando o som situa-se no intervalo mencionado acima, a vibração do tímpano gera uma corrente elétrica, um estímulo, que será enviado ao cérebro. A estes estímulos físicos mensuráveis correlacionamos sensações mentais. Fisicamente, no espectro sonoro podem ser detectadas uma freqüência, uma amplitude e uma composição de diferentes senóides, todas múltiplas da fundamental. A cada um desses parâmetros físicos está associada uma receita que ajuda na interpretação mental dos sons quanto à sua altura, à sua intensidade e ao seu timbre, respectivamente.
Podemos então fazer dois tipos de análise sobre o som. Uma delas é a análise qualitativa, que descreve as propriedades sonoras em termos da nossa percepção., conforme a receita mencionada acima. Esse tipo de análise não pode ser quantificado e, muitas vezes, modifica-se de acordo com as nossas emoções. A outra forma, matemática, descreve as propriedades físicas do som e é perfeita e unicamente mensurável. Vamos começar a nossa análise pela parte qualitativa, associando em seguida a percepção (propriedades qualitativas) às grandezas físicas correspondentes.
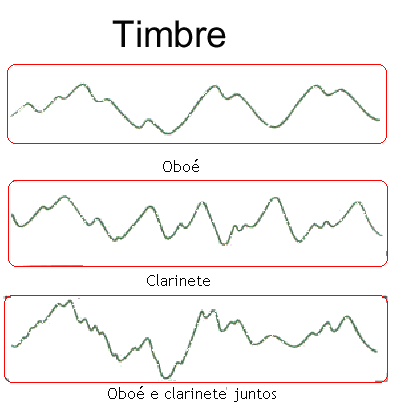
Como dissemos, em termos preceptivos, o som pode ser descrito em termos da sua altura, timbre e intensidade. O timbre está associado à qualidade do som. Ele pode ser comparado a uma "receita mental" para distinguir sons complexos (formados por uma superposição de diversos sons relacionados entre si). Sons provenientes de instrumentos diferentes são perfeitamente distintos, mesmo que exatamente a mesma nota musical seja tocada, uma vez que eles possuem diferentes "receitas de composição". O timbre está associado à série harmônica do som, onde cada nota musical é composta de uma nota fundamental e uma combinação de harmônicos superiores com diferentes freqüências (múltiplas da freqüência fundamental), diferentes intensidades e diferentes durações.
A altura está ligada à percepção de mais agudo e mais grave. Quanto mais alto é um som, mais agudo ele é. Esta diferenciação é baseada nas variações da freqüência de vibração destes sons. Aos sons graves relacionam-se as baixas freqüências e aos agudos as altas. É importante deixar claro que a freqüência (o número de ondas completas ou ciclos por segundo) é um conceito objetivo e pode ser CIENTIFICAMENTE MEDIDO. A altura do som depende da percepção sonora de quem está ouvindo o som e é bastante subjetivo. Entretanto, a relação direta entre os dois pode ser claramente percebida.
Quanto à intensidade pode-se dizer que um som é forte ou fraco. Nossa percepção de intensidade é, talvez, a que mais se aproxime da grandeza física, uma vez que estamos simplesmente percebendo a "quantidade de som" que chega até nossos ouvidos. A correlação é estabelecida ao interpretarmos a intensidade como a quantidade de energia sonora que chega aos ouvidos humanos, ou seja, classifica-se como mais fortes os sons provenientes de vibradores que oscilem em maiores amplitudes exercendo assim uma maior pressão sobre o ar.
Pelo que já falamos, você deve estar percebendo que o som é bastante afetado pelas condições do ambiente. Quando percebemos um som, diversos fatores externos à fonte sonora influenciam na qualidade deste: as paredes e as propriedades de seu revestimentos, o volume de ar da sala, a densidade do ar, a umidade, o coeficiente de reverberação do recinto, etc. Portanto, uma fonte sonora não produz o mesmo som em ambientes diferentes, principalmente se esta fonte for um instrumento musical. Nesse caso, ele está sempre sujeito a alterações de timbre e volume quando submetido às alterações climáticas. As ondas sonoras, ao deixarem a fonte, sofrem uma série de alterações qualitativas. A maior interferência porém, se dá a nível da interpretação humana dos sons. Nesta interpretação estão envolvidos a estrutura mecânica do ouvido, a estimulação cerebral e os elementos da memória sonora. Devido à natureza destes fatores a percepção e a qualificação dos sons são inexoravelmente subjetivas. O mesmo som pode soar completamente diferente para dois indivíduos dispostos no mesmo ambiente acústico.
Da mesma forma, a escolha de um bom instrumento musical é algo extremamente delicado, uma vez que a análise de sua qualidade sonora pode ser comprometida em função do local em que ele se encontra, ou das condições climáticas da época, além da percepção sonora da pessoa que toca o instrumento. É interessante ressaltar que a percepção do timbre e do volume, embora subjetiva, está relacionada com a série harmônica e com a quantidade de energia sonora gerada por um instrumento musical. Assim, sutilezas sonoras podem ser detectadas fisicamente, mas não serem percebidas por dois instrumentistas tocando o mesmo instrumento. Entretanto, sempre que ambos notarem algo diferente no instrumento, é certo que a análise física também mostrará algum tipo de diferença.
9 – Intervalos e Raiz Harmônica
Se tomarmos duas notas musicais, a primeira mais grave, com uma freqüência de m Hz e uma mais aguda, com freqüência de n Hz, o intervalo entre elas é, por definição, a razão n/m, em que m e n são números inteiros. A Tabela 1 mostra, como exemplo, uma relação entre diferentes notas musicais, partindo do Dó 2 (a segunda nota Dó na escala do piano):
Tabela 1 – Relação entre notas musicais e intervalos para a nota Dó
|
Notas componentes |
|
Nome do intervalo |
|
Dó 2 – Dó 3 |
Oitava |
|
|
Dó 3 – Sol 3 |
3:2 |
Quinta perfeita |
|
Sol 3 – Dó 4 |
4:3 |
Quarta perfeita |
|
Dó 4 – Mi 4 |
5:4 |
Terça maior |
|
Mi 4 – Sol 4 |
6:5 |
Terça menor |
Essa razão entre as freqüências e as alturas dos sons pode ser determinada no comprimento das cordas de uma harpa, no tamanho da coluna de ar dentro de uma flauta ou de um fagote e ao se olhar dentro da caixa de um piano: as cordas mais curtas e as menores colunas de ar corresponderão sempre aos sons mais agudos e vice-versa.
Uma forma de analisar o conceito de intervalo é pensarmos em freqüências relativas. O ouvido humano está mais preparado para "entender" relações (ou diferenças) entre freqüências do que para identificar uma nota solta. Por isso, ao tocarmos uma determinada nota no piano, por exemplo, é difícil, mesmo para músicos profissionais, saber se aquela nota é um Dó, um Dó# ou um Sib. E mesmo os ouvidos mais treinados (os chamados ouvidos absolutos), capazes de perceber essa diferença, não tem condições fisiológicas de distinguir intervalos inferiores ou iguais a 81/80, ou 1,0125, a chamada coma. Essa limitação fisiológica leva a duas conseqüências importantes na Música. A primeira é que, embora exista um número infinito de freqüências (um "continuum"), somente é possível definir um número finito de intervalos perceptíveis ao ouvido humano, a partir das 1400 freqüências discretas mencionadas na seção anterior. Isso leva à noção de escala musical, que discutiremos adiante. A outra é que, dentro do intervalo de uma coma, uma pequena "desafinação" é perfeitamente tolerável.
O conceito de raiz harmônica está diretamente ligada ao conceito de interferência. Se tocarmos duas notas musicais com freqüências de m Hz e n Hz, a sua raiz harmônica é uma nota mais grave, produzida pela interferência (ver seção 6) entre elas, dada pelo máximo divisor comum das duas. A raiz harmônica da combinação do Dó 3 (264 Hz) e do Sol 3 (396 Hz) é o Dó 2 (132 Hz). A sensação que se tem quando tocamos a combinação Dó 3 – Sol 3 é que se está ouvindo um Dó 2 desfalcado de alguns harmônicos, inclusive da nota fundamental. A disciplina da Harmonia é fortemente calcada no conceito de raiz harmônica, que pode ser aplicado à combinação de duas, três ou mais notas musicais.
A proximidade entre a raiz harmônica de um intervalo e a mais grave de duas notas tocadas simultaneamente define o "parentesco" entre essas duas notas. Especificamente, sejam duas notas de freqüências m Hz e n Hz, m e n sendo números inteiros (n > m) e q o máximo divisor comum de m e n. O parentesco entre as duas notas é, por definição, o inteiro m/q. A relação de parentesco entre notas é definida a partir do intervalo entre elas. Genericamente, se este intervalo é expresso pela razão p/q (p > q), o parentesco entre elas é de ordem q. Assim, num intervalo de uma oitava, temos uma relação p/q = 2/1, então o parentesco é de primeiro grau (a segunda nota está inteiramente contida dentro da senóide da primeira); num intervalo de quinta perfeita, a relação é p/q = 3/2, o parentesco é de segundo grau. Na quarta perfeita, p/q = 4/3 e temos um parentesco de terceiro grau e assim por diante.
Pode-se mostrar que a ideia de parentesco tem implicações diretas na combinação de sons, criando os conceitos de consonância e dissonância. Essas relações são resultado das possibilidades discretas para a criação dos cerca de 1400 intervalos comentados anteriormente. Certas combinações, dentro desse conjunto de intervalos, são mais agradáveis ao ouvido humano que outras. E ainda, certas culturas tendem a perceber consonâncias e dissonâncias de forma muito diferente.
10 – As Escalas Musicais
Vamos discutir, nessa seção, as diferenças entre as escalas musicais justas e temperadas, mostrando como a percepção sonora pode influenciar claramente na combinação de instrumentos musicais temperados e não temperados. As escalas musicais são, a rigor, a divisão da seqüência de notas contidas dentro de uma oitava. Essa divisão pode ser feita de diversas formas, obedecendo principalmente a critérios estéticos, quer em termos da melodia que as notas formam, quer em termos das relações harmônicas entre elas. Sem entrar em detalhes no processo da construção das escalas, vemos que a divisão da escala musical em sete notas principais (tom – tom – semitom – tom – tom – tom – semitom) é uma conseqüência da irracionalidade na divisão dos intervalos que definem a escala.
A ideia de parentesco entre as notas (ligada à relação harmônica entre elas) pode ser analisada novamente à luz das séries de Fourier, uma vez que combinações de formas sonoras cujas freqüências não tenham entre si alguma possibilidade de interferência construtiva dentro de uma ou duas oitavas (um ou dois ciclos) quase certamente não formarão nenhum tipo de relação harmônica, pelo menos dentro da estética ocidental. Por exemplo, na escala de Dó maior, alguns intervalos foram arranjados para que se tornassem iguais a 9/8, ou seja, um intervalo de um tom (definido em qualquer livro de acústica). São esses os intervalos dó-ré, fá-sol e lá-si. Já os intervalos ré-mi e sol-lá são iguais a 10/9, ligeiramente inferiores a um tom. Como a diferença relativa entre 9/8 e 10/9 é igual a uma coma, o resultado é imperceptível se arredondarmos os intervalos de 10/9 para 9/8. O intervalo entre mi e fá e si e dó é ligeiramente superior a um semitom, mas também menor que uma coma, logo ele também foi arredondado para 16/15. Isso criou duas assimetrias por causa do arredondamento mencionado acima. Uma assimetria que os músicos chamam de "primeiro grau" e que é próxima de um intervalo de ½ tom; a outra é uma assimetria de "segundo grau" e está relacionado ao intervalo de cerca de uma coma.
A introdução dessas assimetrias apontou para a criação de notas estranhas às presentes na escala de Dó maior. Isso ocorreu para permitir que uma mesma melodia pudesse ser cantada a partir de uma tônica diferente, isto é, mantendo as mesmas assimetrias (a estrutura de 2 tons, um semitom, 3 tons e mais um semitom, presente na escala maior) presentes na escala maior de sete notas. Duas soluções foram criadas para resolver o problema das notas intermediárias. Uma delas foi a introdução das notas alteradas (sustenidos e bemóis), formadas a partir da multiplicação ou divisão da nota original por 25/24. A multiplicação criava uma nota sustenida e a divisão criava uma nota bemol. Com isso a escala de sete notas passava a ter vinte e uma notas, todas elas guardando algum parentesco com a tônica. O intervalo entre duas notas sucessivas nunca excede 25/24, que é menor do que três comas e, portanto, perceptível somente para os ouvidos mais treinados. Assim, qualquer nota imaginável, nos cerca de 1400 intervalos perceptíveis para o ouvido humano, se aproximaria de uma das 21 notas da escala de naturais, sustenidos e bemóis com um erro menor do que uma coma e meia.
A outra solução, ideal para os instrumentos de teclado, foi dividir a afinação e distribuir esse erro, inevitável por causa da forma da divisão da escala, entre notas vizinhas. Dividiu-se a oitava em 12 intervalos rigorosamente iguais à raiz duodécima de 2, ou seja, a razão entre as notas passou a ser de 1,059 entre semitons e 1,122 por tom. Com isso, o dó sustenido se iguala ao ré bemol, o mi sustenido ao fá e o fá bemol ao mi, reduzindo as 21 notas iniciais a 12.
É interessante notar que, devido à distribuição de freqüências ser contínua, essa divisão não alterou em nada a análise física dos sons. Ao medir o espectro sonoro de uma nota musical, vamos observar exatamente os mesmos harmônicos e freqüências que seriam esperados em uma série normal. O que se altera é a definição de ONDE fica a freqüência fundamental. Por exemplo, a alteração de Mi sustenido para Fá bemol faz com que a freqüência da nota fundamental ( já que, na escala temperada, ambos são a mesma coisa e na normal não) seja ligeiramente deslocada para um ponto entre ambas as notas.
Não vamos discutir aqui as vantagens e desvantagens de cada uma das afinações; nosso objetivo é mostrar como elas se relacionam, do ponto de vista da análise de sons. Talvez o único comentário interessante a se fazer é que, na escala justa, as notas guardam sempre uma relação de parentesco com a tônica, uma vez que a construção da escala é feita sempre a partir de uma subdivisão de intervalos racionais. Na escala temperada essa relação de parentesco é rigorosamente nenhuma, uma vez que a relação entre as freqüências são expressas por números irracionais. A sensação de parentesco resulta, na melhor das hipóteses, da ilusão auditiva resultante da falta de sensibilidade a intervalos de uma ou duas comas. A Tabela 2 mostra, de forma comparativa, a diferença entre as freqüências e as relações entre notas nas escalas justa e temperada. Note-se a existência de intervalos na escala justa que foram simplesmente eliminados na escala temperada, por uma questão de simplificação.
Tabela 2 – Relação entre as notas musicais, intervalos e freqüências correspondentes
(Adaptada da referência 1)
|
Nota musical |
Intervalo com a nota fundamental |
Afinação natural |
Frequência (Hz) |
Afinação temperada |
Frequência (Hz) |
| Dó | Dó uníssono | 1/1=1,000 | 132,000 | 1,000 | 132,000 |
| Dó # | Semitom | 25/24=1,042 | 137,544 | 1,059 | 139,788 |
| Ré b | Segunda diminuta | 27/25=1,080 | 142,560 | 1,059 | 139,788 |
| Ré | Segunda maior | 9/8=1,125 | 148,500 | 1,122 | 148,104 |
| Ré # | Segunda aumentada | 76/74=1,172 | 154,704 | 1,189 | 156,948 |
| Mi b | Terça menor | 6/5=1,200 | 158,400 | 1,189 | 156,948 |
| Mi | Terça maior | 5/4=1,250 | 165,000 | 1,260 | 166,320 |
| Fá b | Quarta diminuta | 32/25=1,280 | 168,960 | 1,260 | 166,320 |
| Mi # | Terça aumentada | 125/96=1,302 | 171,864 | 1,335 | 176,220 |
| Fá | Quarta perfeita | 4/3=1,333 | 175,956 | 1,335 | 176,220 |
| Fá # | Quarta aumentada | 25/18=1,389 | 183,348 | 1,414 | 186,648 |
| Sol b | Quinta diminuta | 36/25=1,440 | 190,080 | 1,414 | 186,648 |
| Sol | Quinta perfeita | 3/2=1,500 | 198,000 | 1,498 | 197,736 |
| Sol # | Quinta aumentada | 25/16=1,563 | 206,316 | 1,587 | 209,484 |
| La b | Sexta menor | 8/5=1,6 | 211,200 | 1,587 | 209,484 |
| Lá | Sexta maior | 5/3=1,667 | 220,044 | 1,682 | 222,024 |
| Lá # | Sexta aumentada | 152/72=1,737 | 229,284 | 1,782 | 235,224 |
| Si b | Sétima menor | 9/5=1,800 | 237,600 | 1,782 | 235,224 |
| Si | Sétima maior | 15/8=1,875 | 247,500 | 1,888 | 249,216 |
| Dó b | Oitava diminuta | 48/25=1,920 | 253,440 | 1,888 | 249,216 |
| Si # | Sétima aumentada | 125/64=1,953 | 257,796 | 2,000 | 264,000 |
| Dó | Oitava perfeita | 2/1=2,000 | 264,000 | 2,000 | 264,000 |
A figura abaixo mostra as relações entre as freqüências e os intervalos na escala temperada e justa. Pode-se ver claramente as irregularidades e a quebra de um comportamento linear na afinação temperada. Basicamente a curva irregular quer dizer que estamos chamando dois sons diferentes (duas freqüências diferentes) pelo mesmo nome.
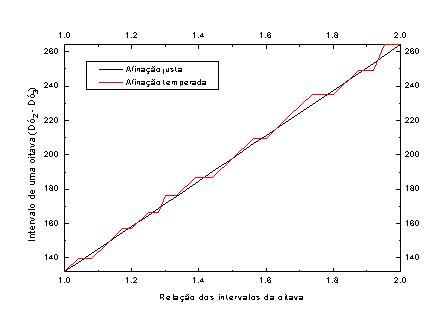
O grande problema ligado às escalas diferentes encontra-se quando instrumentos temperados como o piano e o violão tocam com instrumentos não temperados, como o violino, por exemplo. A única coisa a ser feita, nesse caso, é o violinista ouvir e ajustar a nota tocada ao temperamento do outro instrumento, para que não haja um choque harmônico muito grande.
11 – Instrumentos Musicais e Suas Características Físicas
Cada tipo de instrumento tem uma espécie de "assinatura", um conjunto de características sonoras associado que, embora possa parecer subjetivo, tem uma descrição matemática extremamente precisa. Anteriormente comentamos que o som pode ser representado pela soma de diversas ondas individuais, que chamamos de componentes de Fourier. O que diferencia um instrumento de outro são as amplitudes e a duração de cada um dos harmônicos presentes no som resultante; a esse conjunto de características chamamos timbre.
A altura de um som está ligada à intensidade com que ele é emitido, ou seja, ao volume sonoro deste som. Em termos físicos, a altura está ligada à amplitude da onda sonora gerada pela vibração de um determinado instrumento ou material. Quanto maior a amplitude da onda, maior é a quantidade de energia que ela carrega, consequentemente, maior é o seu volume.
Entretanto, a altura pode ser também tratada como a "afinação" de um som. Ela é um atributo do sistema auditivo humano a partir do qual sons quaisquer podem ser classificados em uma ordem que vai do mais baixo ao mais alto, como numa escala de notas musicais. A relação entre a altura e a afinação está ligada à freqüência de vibração do objeto que gerou esse som.
As ondas sonoras complexas geradas por um instrumento musical sempre poderá ser representada por uma série de Fourier, compostas das nota fundamentais e da série de harmônicos ou sobretons, cada um com a sua amplitude e fase. A expressão matemática de uma onda complexa poderia ter a seguinte forma:
P = sen w t + 1/2 sen 2w t + 1/3 sen 3w t + 1/4 sen 4w t + 1/5 sen 5w t.
A Figura 4 mostra as componentes individuais e o resultado das somas de todas (P) e da soma de somente os harmônicos ímpares.
a)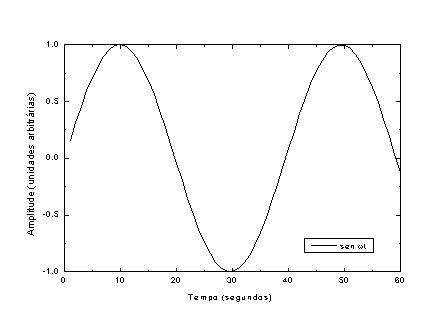 b)
b)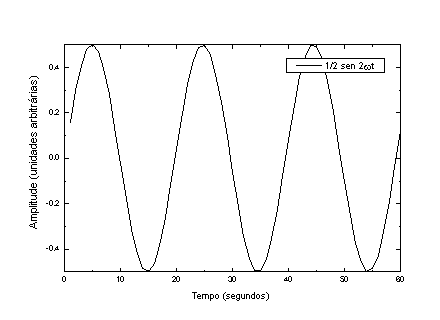
c)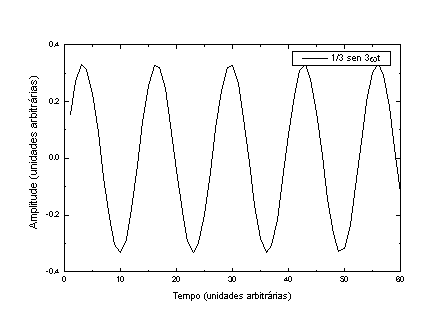 d)
d)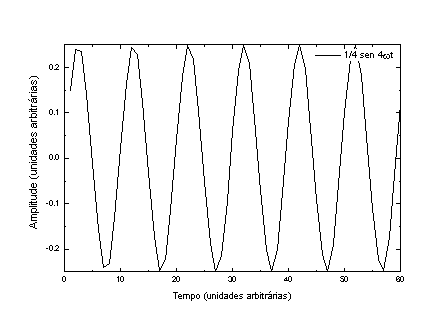
e)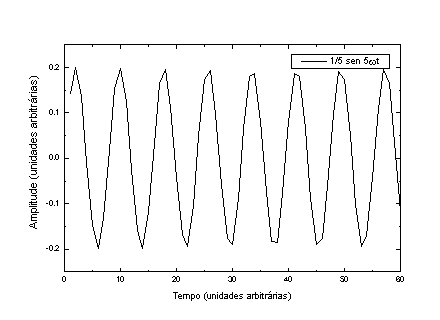 f)
f)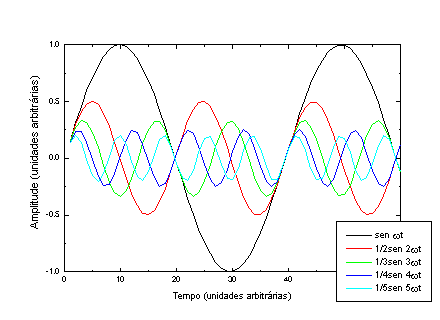
g)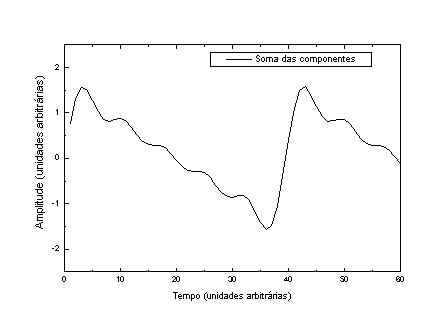
Figura 4 – De cima para baixo, as componentes harmônicas da onda representada na página anterior. Em a), b), c), d) e e) temos as componentes individuais, em f) temos todas colocadas na mesma figura e em g) temos a soma das 5 componentes.
A estrutura de uma onda sonora produzida por um instrumento pode ser extremamente complexa. Qual seria o tipo de onda produzido pelas séries abaixo?
| P = cos w t + 0,7 cos 2w t + 0,5 cos 3w t | (5.1) |
| P = senw t – 0,5sen3w t + 0,33sen5w t – 0,25sen7w t | (5.2) |
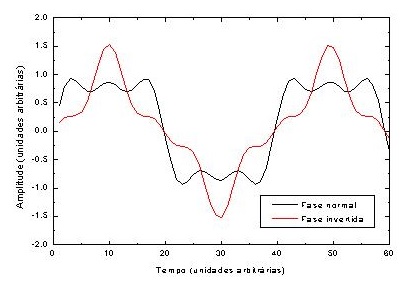
Figura 5 – Soma dos harmônicos em fase (preto) e em fase invertida (vermelho), de acordo com as equações acima
A fase de uma componente desempenha um papel importantíssimo na determinação da forma da onda resultante. Por exemplo, nas expressões abaixo (vistas na Figura 5) notamos que a fase do terceiro harmônico da segunda expressão está invertida de 180 graus em relação à primeira. Observe como a diferença é notável.
Em geral, exceto por mudança de fases muito grandes, como foi o caso acima, ou sons muito intensos, a fase não é muito importante na determinação da forma da onda.
O espectro sonoro é uma forma de mostrar a estrutura de uma onda complexa. Ele é capaz de mostrar quais são as freqüências principais que constituem um determinado som. Então, ao invés de um gráfico onde temos a amplitude em função do tempo, como nas Figuras 4 e 5, teremos um gráfico de amplitude x freqüência. Um exemplo desse gráfico espectral pode ser visto na Figura 6.
O que diferencia um instrumento do outro é exatamente a distribuição de freqüências e das formas de ondas que vimos nas figuras anteriores. Pode-se ver no laboratório que instrumentos de corda são, em geral, bem mais ricos em termos de harmônicos e possuem a forma de onda mais complexa. Os mais pobres são, tipicamente, os de percussão e alguns dos metais (a flauta é o melhor exemplo dos metais, por praticamente não apresentar termos harmônicos de ordem superior a 2, quando ela toca uma nota de freqüência igual a 1568 Hz).
Vamos encerrar esta seção comentando as freqüências fundamentais de ressonância de diversos instrumentos. Elas são características de cada instrumento e dependem, como veremos abaixo, das peculiaridades de cada um. Sistemas acionados por cordas vibrantes possuem uma freqüência fundamental que depende da tensão, massa e comprimento da corda.
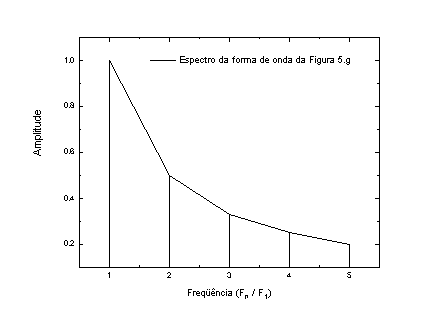
Figura 6a – Espectro sonoro da primeira equação dos senos (5.1)
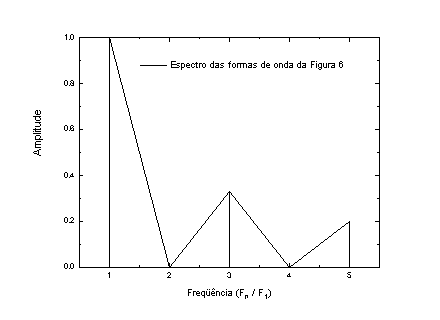
Figura 6b – Espectro sonoro da segunda equação dos senos (5.2)
Membranas vibrantes e discos metálicos, típicos de instrumentos de percussão, possuem um padrão de freqüência fundamental que é típica e parecida uma com a outra, dependendo também da tensão e densidade da membrana. Já tubos sonoros dependem exclusivamente do comprimento da coluna de ar contida no tubo. A Tabela 3 mostra essa relações para diversos ressonadores, inclusive tubos de órgãos metálicos, e a nomenclatura de cada termo. Os termos referentes aos módulos de Young e razão de Poisson podem ser encontrados em qualquer livro texto clássico de Mecânica e oscilações. Os valores são, por uma questão de concordância, dados no sistema de unidades CGS.
Tabela 3 – Relação entre elementos vibradores e suas freqüências de ressonância
(Adaptado da referência 3)
|
Elemento vibrador |
Frequência |
Componentes |
|
Cordas |
f = 1/(2l) (T/r )1/2 |
l = comprimento da corda |
|
T = tensão |
||
|
r = densidade linear |
||
|
Barra vibrante presa em um das pontas (vibração transversal) |
f = 0,5596/l2 (QK2/r )1/2 |
l = comprimento da barra |
|
Q = módulo de Young |
||
|
K = |
||
|
r = densidade linear |
||
|
Membranas esticadas |
f = 0,382/R * (T/r )1/2 |
R = raio da membrana |
|
T = tensão |
||
|
r = densidade linear |
||
|
Pratos circulares presos nas bordas |
f = 0,467t/R2(Q/r (1-s 2)1/2 |
t = espessura da placa |
|
R = raio da placa |
||
|
r = densidade linear |
||
|
s = razão de Poisson |
||
|
Q= módulo de Young |
||
|
Pratos circulares presos no centro |
f = 0,193t/R2(Q/r (1-s 2)1/2 |
t = espessura da placa |
|
R = raio da placa |
||
|
r = densidade linear |
||
|
s = razão de Poisson |
||
|
Q= módulo de Young |
||
|
Barras vibrantes (vibração longitudinal) |
f = 1/(2l) (Q/r )1/2 |
l = comprimento da corda |
|
Q = módulo de Young |
||
|
r = densidade linear |
||
|
Órgãos e tubos |
f = c/2xl (aberto) |
l = comprimento do tubo |
|
f = c/4xl (fechado em um dos lados) |
c = velocidade do som |
12 – Conclusão
Nosso objetivo nesse texto foi apresentar, mesmo que de forma superficial, alguns dos princípios em que a Acústica se baseia, os mecanismos de produção de som, o conceito (nada trivial de ser entendido sem a devida estrutura matemática) das séries e da análise de Fourier e algumas das diferenças entre sons diversos e sons musicais.
Naturalmente, uma série de tópicos deixou de ser discutido em detalhes aqui, como ressonância, batimentos e, com certeza, muitos outros que você gostaria de ver incluído. Entretanto, meu objetivo, ao ligar diretamente a Física e a Música, foi tentar fornecer algumas ferramentas que nos permitisse distinguir entre os diferentes instrumentos musicais a partir da análise da sua série harmônica – em suma, tentar determinar a sua "assinatura sonora" e mostrar como a Física está direta e intimamente ligada aos detalhes da percepção musical, como a sensibilidade a harmônicos específicos ou as diferentes maneiras de se perceber o que é agudo e grave, ou alto e baixo. Minha formação musical ajudou e influenciou um pouco na escolha de alguns tópicos em detrimento de outros. Entretanto, esse trabalho será certamente revisto para apresentação em outras situações e condições. Releia o material pensando em algo que você gostaria que fosse incluído e, caso deseje, entre em contato comigo. O seu comentário será extremamente valioso para que esse material seja incrementado e melhorado.
Por fim, é interessante comentar as distâncias que separam (ou seria melhor dizer: aproximam?) a Física da Música. Uma forma de arte nunca será objetiva e precisa a ponto de ser uma unanimidade, mas as simetrias e belezas observadas nas leis que governam a combinação das estruturas matemáticas usadas na descrição dos sons, em geral, e que permitem analisar o espectro sonoro de cada instrumento musical guardam estreita relação com a área da Música conhecida como Harmonia. Dessa maneira, a Física e a Matemática também são capazes de mostrar e descrever, a partir de uma abordagem objetiva, as possibilidades das infinitas combinações de sons criadas por um gênio como Johann Sebastian Bach, por exemplo. A delicadeza das construções sonoras dos grandes mestres da Música pode ser vista, ao invés de ouvida, na análise dos sons de suas obras e no perfeito equilíbrio entre as formas de ondas instintivamente combinadas para formá-las. Ao ouvir algumas das "obras canônicas" dos compositores famosos, considero-os privilegiados por serem capazes de expressar e/ou criar emoções e "imagens sonoras" tão belas, algumas perpetuadas através dos séculos, que puderam ser transmitidas a outros através da arte da Música. Ao mesmo tempo, ao estudar a História da Ciência, considero não menos privilegiados alguns dos físicos e matemáticos mais importantes da História. A eles coube o prazer de descobrir leis e fenômenos naturais, nos deixando ferramentas poderosas para o entendimento dessa mesma Natureza. É a perfeição dessas ferramentas e leis que nos permite olhar a Música sob outra óptica, um prisma diferente, unindo os mundos maravilhosos da Arte e da Ciência.
Bibliografia
Existe uma enorme carência de material escrito sobre o assunto dessa monografia em língua portuguesa; já em inglês, trabalhos diversos, livros, teses e dissertações são mais facilmente encontrados. Colocarei, sem nenhuma ordem de preferência ou importância, o material consultado durante a preparação do texto.
- "Ensaios Analíticos" (Mario Henrique Simonsen), cap. 5. Editora da Fundação Getúlio Vargas, 2ª edição, Rio de Janeiro/RJ, 1994.
- "Dicionário Grove de Música – Edição concisa" (Editado por Stanley Sadie). Jorge Zahar Editora, Rio de Janeiro/Brasil, 1994.
- "Exploring music: the science and technology of tones and tunes" (Charles Taylor). Institute of Physics Publishing, Philadelphia/EUA, 1992.
- "Music, Physics and Technology" (Harry Olson). Dover Publications, Inc., 2nd edition, New York/USA, 1967.
- "Treatise on harmony" (Jean Phillipe Rameau). Dover Publications, Inc., New York/USA, 1971.
- "How things work – the physics of everyday life" (Louis P. Bloomfield). John Wiley & Sons, Inc., New york/USA, 1997.
- "Waves – Berkeley Physics Course, vol. 3" (Frank S. Crawford, Jr.). McGraw Hill Book Company, New York/USA, 1973.
- "O som e o sentido" (João Miguel Wisnick). Companhia das Letras, 2ª edição, 1998.
- "The Physics of the Musical Instruments" (N. Fletcher e T. Rossing), Springer, 2ª edição, 1998.
- "Física e Psicofísica da Música" (Juan Roederer), Edusp, 1998 (2a. reimpressão: 2002)
Carlos Alexandre Wuensche de Souza é pesquisador da Divisão de Astrofísica do
INPE
Fonte: http://www.das.inpe.br/~alex/FisicadaMusica/fismus_introducao.htm









