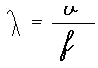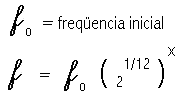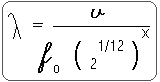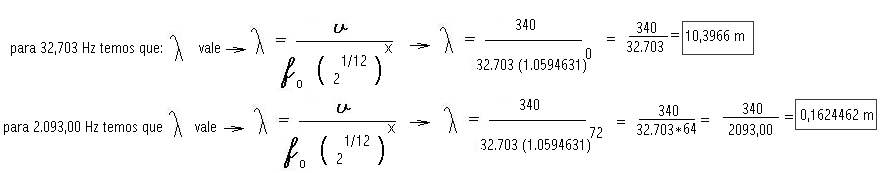por: Prof.Luiz Netto
|
Thomas Alva Edison, e uma de suas magnificas invenções – O “phonógrafo”. |
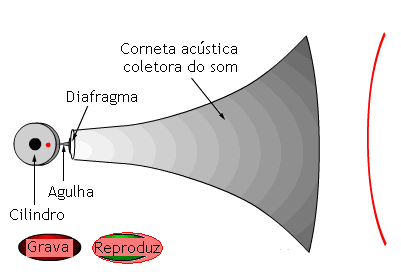
Quem quer que ja tenha ouvido o som que sai de de uma daquelas antigas vitrolas acústicas deve ter ficado espantado e maravilhado com o volume de som forte que sai daquela magnífica corneta acústica. Nos meus tempos de criança, quando eu ia ao sitio de minha avó em Piquerobi, SP – a única diversão que lá havia era uma dessas vitrolas, bem como um rádio (Marca Belmonte) – cuja fonte era uma enorme pilha que era trocada mais ou menos a cada 4 ou 5 meses, ao redor do qual ficava toda família a ouvir os programas de ondas curtas de música sertaneja.
Lembro-me de um famoso trio sertanejo sempre presente – Torres, Florêncio e Rielli Filho, cujas musicas estávamos acostumados a ouvir com prazer no vaivém do “fading” causado pela flutuação da camada ionosférica, variando o nível de audibilidade ao sabor dessa dança. Ao término do programa cantavam eles: “Até segunda-feira minha gente…Até lá nois vortamo aqui cantá…“ Após ouvir o rádio, meu tio armazenava energia na corda da vitrola e punha aqueles discos – que sempre ao inicio se ouvia a fala do locutor: “Casa Edson – Rio de Janeiro”.
Perguntava-me então com a curiosidade de uma criança como era possivel que aquela enorme agulha grossa ao percorrer a trilha do disco vibrando ao sabor das sinuosidades do sulco gravado – conseguia extrair um volume de som tão alto, sem que houvesse meios eletrônicos de amplificação. Eu não tenho especialidade nesta área, mas como procurei e não achei em livros de física explicações didáticas dos fundamentos para saber como funcionaria uma corneta acústica resolvi trabalhar alguns conceitos de física que reestudei em meus livros para ver onde poderia chegar para compreender melhor o porque este formato de perfil de uma curva exponencial consegue ser uma câmara de ressonância(*) para as frequencias de áudio ali introduzidas. Então, vamos lá:
|
Temos que estudar como varia o comprimento de onda
Vamos verificar como varia a frequencia. Por uma questão mais didática vou considerar aqui as frequencias das notas musicais com valores numéricos dados pontualmente ao longo escala musical temperada, percorrendo as sucessivas oitavas. Antes vamos fazer algumas considerações para entender como vamos colocar o valor de f.
Assim podemos escrever que:
Então:
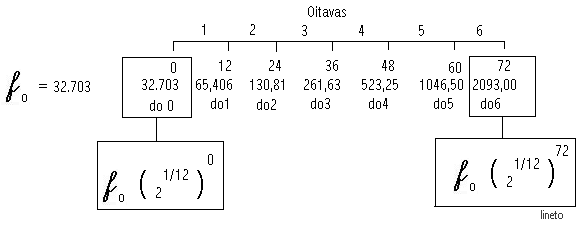
Esta é a fórmula que utilizaremos para cálculo dos Comprimentos de Ondas Portanto, f de índice zero determina a frequencia mais grave de corte e a frequencia mais aguda é determinada pelo expoente x de ordem 72 – (f final) Consideremos uma extensão de seis oitavas, tomando como frequencia inicial (f de corte) a nota dó correspondente a 32,703 Hz, e calculemos qual a faixa de comprimento de onda correspondente para essa frequencia inicial e a final.
Vamos tomar como parâmetro de velocidade do som no ar como sendo 340 metros por segundo, correspondente à temperatura de 14.1 graus Celsius- (**). Para outras temperaturas utilize a fórmula para cálculo indicada ao fim desta página. Assim como veremos mais abaixo teremos o comprimento de onda para 32,703 Hz uma onda de 10,3966 metros e para a frequencia de 2.093,00 Hz o comprimeto de onda de 0,1624 metros ou 16 centímetros.
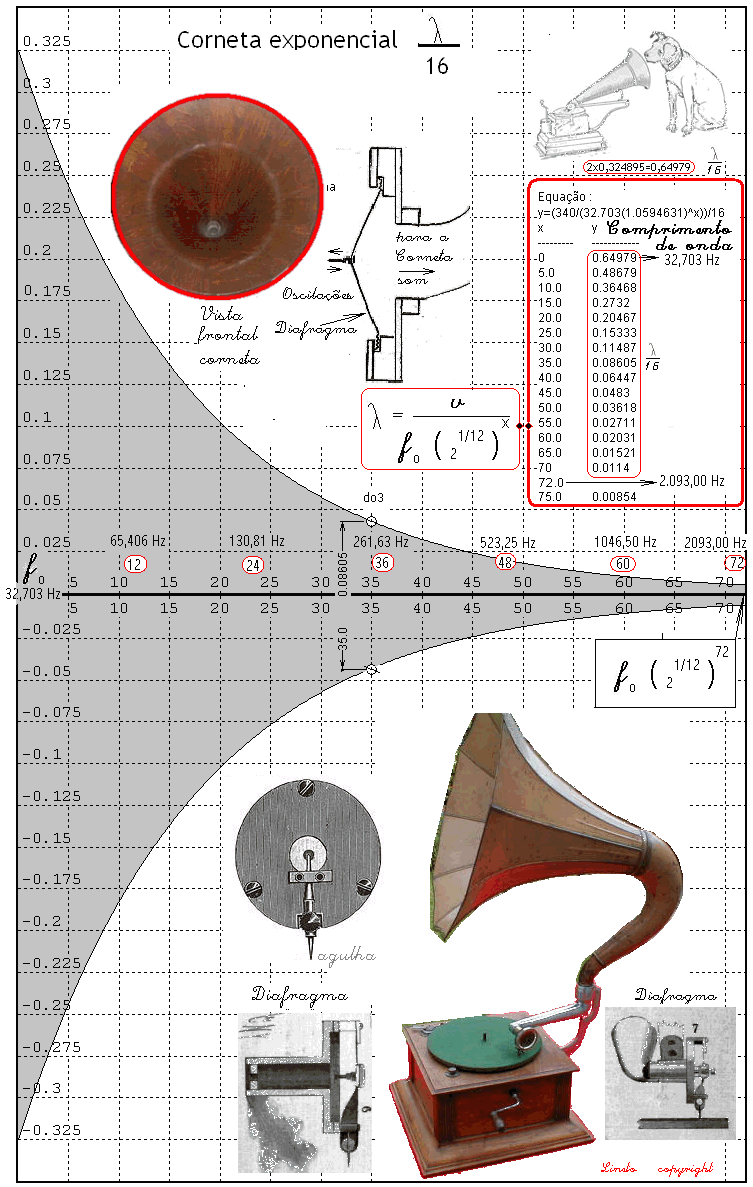
As ondas sonoras podem ressoar em tubos com submultiplos do comprimento de onda. Se fossemos construir uma corneta acústica com essas dimensões seria uma corneta enorme como podem ver. Assim, vejamos como seria a variação dos comprimentos de ondas das frequencias compreendidas entre 32,703 Hz e 2093,00 Hz, escolhendo um submultiplo tal que a medida maior fique ao redor de 60 centímetros. Experimentemos:
Assim para a frequencia de 32.703 Hz teremos um comprimento de 10,3966/16 = 0,6497875 = 65 centímetros e para a frequencia de 2.093,00 Hz teremos um comprimento de onda de 0,162442/16 = 0,0101526 m ou UM centímetro.
O diafragma: É o dispositivo que transforma as variações de movimento colhidos pela agulha nos correspondentes movimentos de uma membrana.A agulha ao percorrer o sulco do disco que contém a informação de áudio vibra – sendo que este movimento oscilatório move o diafragma de modo que isto movimenta a coluna de ar dentro da corneta nas frequencias que variam em função do tempo, sendo que as distancias ao longo da curva exponencial variam com os submultiplos dos comprimentos de ondas correspondentes.
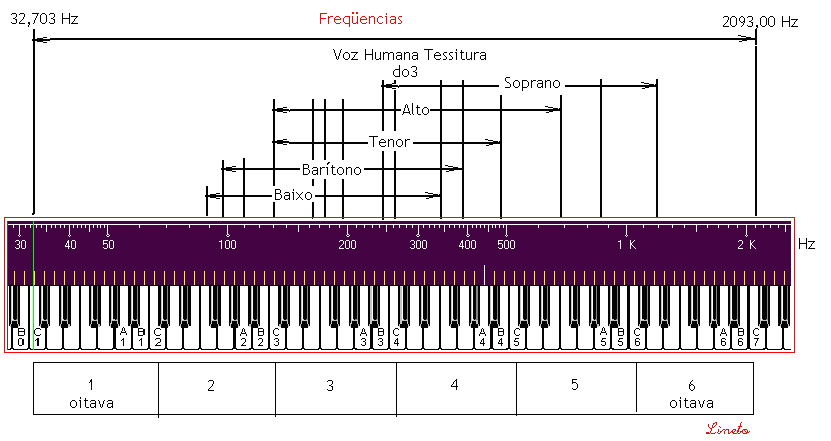
Tessituras – Alcance da voz humana Como sabemos a faixa de percepção do ouvido humano é ao redor de 20 à 20.000 Hz e vemos que esta corneta contempla também o extremo dos agudos de uma voz soprano, ao redor de 1,2 Khz. FREQUENCIAS DADAS EM Hertz e COMPRIMENTOS DE ONDAS DADOS EM metros.
Contudo, olhando para a tabela acima, verique que as frequencias que vão desde 32,709 Hz até 16743,98 Hz tem seus comprimentos de onda contemplados nas secções da corneta acústica, ora como função de um inteiro de comprimento de onda ou de fração de comprimento de onda. Uma experiência interessante será gerar um sinal de frequencia conhecida, correr um minúsculo microfone ao longo do eixo central, registrar esses sinais, medir os valores em db e comparar os valores medidos ao longo do eixo.
Planos de secção na Corneta Acústica
*(Ressonância): Quando as cordas de um violão estão afinadas (Mi, La, Re, Sol, Si, Mi), ao apertar o quinto traste da sexta corda (a corda do “Misão”) , percebe-se que a quinta corda (La) começa vibrar simultâneamente com a sexta corda. A energia comunicada à corda (La) é que faz com que ela também vibre, diz-se que ela entrou em ressonância. Mesmo que se interrompa a emissão do som pela sexta corda, a quinta corda (La) continuará ainda a vibrar alimentada pelas vibrações que também estão em ressonância dentro da caixa acústica do instrumento. Assim, dentro do espaço circunscrito dentro da corneta há uma coluna de ar vibrando com diversos comprimentos de onda, que após o limite da borda espalha-se. Essas vibrações são realimentadas continuamente pela fonte, o (diafragma), que reforça a amplitude desses sinais, nos pontos onde as secções na corneta correspondem a múltiplos e submultiplos dos comprimentos de ondas emitidas.
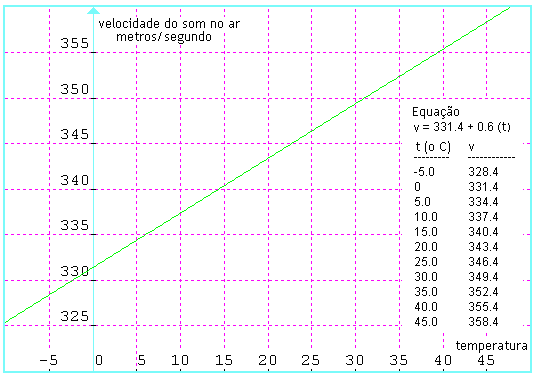
(**) – (Velocidade do som no ar) Ar é uma mistura relativamente fixa de gases e consiste principalmente de Nitrogênio, Oxigênio, Argônio e Dioxido de Carbono. Também inclui quantias variadas de vapor de água ou umidade. Um aumento na quantia de umidade no ar aumenta um pouco a velocidade do som. Desde que umidade pode variar tanto, e como a quantia de mudança de velocidade com uma mudança extrema em umidade é menos os 0.5%, normalmente é medida simplesmente a velocidade de som em ar em ar seco e se negligencia o efeito de umidade. Equação para a velocidade do som no ar A velocidade do som no ar seco em metros por segundo (m/s) é aproximadamente igual a: v = 331.4 + 0.6TCm/s onde v = velocidade do som no ar Assim, se TC = 0oC, então v = 331.4 m/s. Abaixo uma tabela relacionando temperatura x velocidade:
Quero dizer que esses valores calculados para a corneta acústica eu pude constatá-los muito próximos através das medidas que levantei em uma Corneta Exponencial de propriedade um amigo aficionado dessas vitrolas acústicas antigas. Esse artigo aqui tem a finalidade única e exclusivamente de dar uma ideia inicial de como isto funciona. Há estudos profundos sobre este assunto. Encontrei na internet este sitio: – (Horn Theory Article) – http://www.quarter-wave.com/Horns/Horn_Theory.html cujo tratamento matemático é mais complexo. Nosso enfoque é com o sentido de fazer uma primeira abordagem mais para delinear uma primeira concepção de seu funcionamento, utilizando os conceitos de física estudados no segundo grau. Se consegui meu objetivo, dou-me por satisfeito. Mais tarde com outras ferramentas matemáticas mais avançadas poderão dar outro tratamento a estas questões. Com estes estudos simples desta página tento interessar e motivar os nossos estudantes para os estudos das ciências. Digo das ciências porque hoje se percebe que não se pode colocar o conhecimento em compartimentos estanques fechados, em um determinado conhecimento há partes que envolvem a física, a matemática, a biologia, etc. Neste caso por exemplo que estamos estudando poderíamos ver como se processa a recepção de áudio estudando na biologia o funcionamento da cóclea, saber como esta funciona como um discriminador de frequencias… Percebe-se uma nítida interpenetração entre as várias disciplinas. Há muita coisa que pode ser estudada de um modo simples e é isto que deve ser incentivado afim de que não se perca o entusiasmo e a vontade de conhecer, saber, aproveitando todo o tempo que dispomos, para que continuemos nos maravilhando por toda a nossa vida. FREQUENCIA X PERÍODO – NOTAÇÃO POLAR
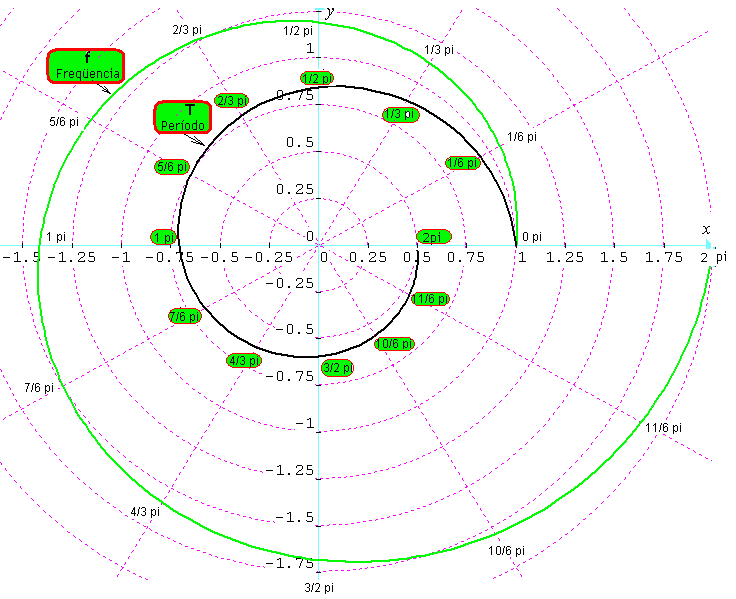
Frequencia x período – Notação Polar – Representação de 1 oitava – Cada 30 graus – (1/6 pi) – um semiton Período é o inverso da frequencia -> T = 1/f – Tempo de duração de 1 ciclo Equação utilizada r = (2^(1/12))^(1.9098593t) r = frequencia, t=expoente – variando de zero a 12 – (12 intervalos da escala musical igualmente temperada) 12/2pi(t) = K(t)-> 1.9098593(t) = kt -> kt = 1.9098593t ^ -> significa elevado a… VARIAÇÃO DO COMPRIMENTO DE ONDA AO LONGO DAS SEIS OITAVAS
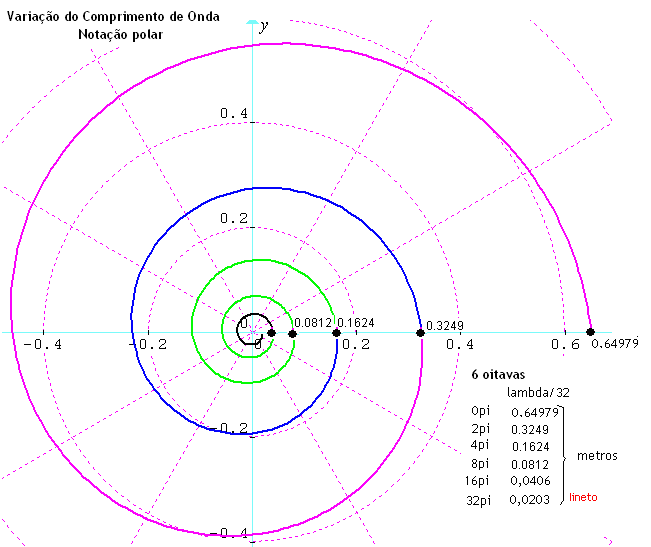
Variação do Comprimento de Onda – Notação Polar r =((340/(n(32.703((1.0594631)^(1.9098593t))))/16)) faça n=1,2,4,8,16,32 -> r (Comprimento de onda) – lambda. Estes valores numéricos obtidos só são válidos em se considerando a velocidade de propagação do som no ar como sendo 340 metros por segundo. |
Consultas:
1) – Elementos de Física: General y experimental
Calor – Movimiento Vibratório – Acustica
M.F.Gran-Prof. titular de Física Superior de la Universidad de La Habana.
2) – Curso “Esse de Alta Fidelidade”
Eng. Helio Taques Bittencourt
Eng. Paulo Taques Bittencourt
3) – Oscilações – Ondas Acústicas
Eng. Tore Nils Olof Folmer-Johnson
4) – Calor e Acústica – L.P.Maia
5) – Tratado de Física Elementar
Francisco Ribeiro Nobre
Lello & Irmão – PORTO – PORTUGAL
6) – Equações Vallumbrosianas
Bernardus Vallumbrosius (1861-1928)
Programas Gráficos:
Programa Graphmatica
http://graphmatica.com/
Áudio:
Cool Edit
https://www.softpedia.com/get/Multimedia/Audio/Audio-Editors-Recorders/Cool-Edit-Pro.shtml
FFT MUSEV: Análise de Spectro
http://artemis.ffclrp.usp.br/softwareP.htm
Teoria da Corneta Exponencial na Internet
http://www.quarter-wave.com/Horns/Horn_Theory.html
O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil