Matemática na Música – Capítulo 3
Som, Ondas e Números
3.1. O que é o som
De uma forma geral, o som é uma sensação que resulta da percepção de distúrbios das moléculas de um meio num certo intervalo de tempo. Esses distúrbios, por sua vez, propagam-se no meio sob a forma de ondas. O som que ouvimos resulta dum distúrbio na atmosfera causado por um emissor, distúrbio esse que consiste em rápidas variações da pressão atmosférica que se propagam sob a forma de ondas até aos nossos ouvidos. Estas ondas provocam variações na membrana auricular, as quais vão ser transmitidas ao cérebro através de pequenos choques elétricos que provocam a percepção sonora. As ondas de pressão que caracterizam o som são chamadas de ondas sonoras. A velocidade de propagação das ondas sonoras está dependente do meio em que se propagam, sendo maior na água que na atmosfera. Na atmosfera, a velocidade de propagação é independente da pressão atmosférica, variando somente em função da temperatura, sendo diretamente proporcional à raiz quadrada da temperatura em Kelvin. A uma temperatura de 21º C, a velocidade do som corresponde a cerca de 344 ms-1 na atmosfera, 1520 ms-1 no mar e 1558 ms-1 no corpo humano.
Se a variação de pressão que origina o som se repetir consecutivamente e de acordo com um padrão, então estamos na presença de um fenômeno que se designa por uma forma de onda periódica. Um exemplo que ilustra bem este conceito é imaginar o som produzido por uma corda de guitarra:
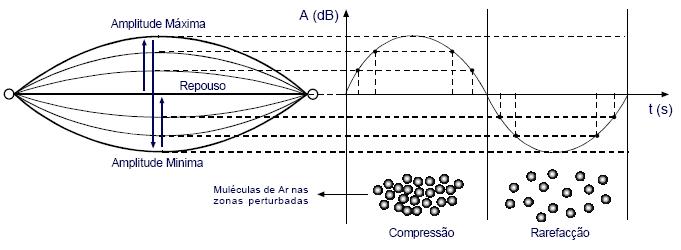
figura 3.1.1: ciclo de uma onda de forma sinusoidal em função do tempo
Imprimindo um impulso inicial à corda é desencadeado um movimento oscilatório que provoca a deslocação entre as posições designadas na figura anterior como Amplitude Máxima e Amplitude Mínima, passando pela posição de repouso. A variação da pressão atmosférica consiste numa compressão e rarefação consecutiva das moléculas de ar localizadas nas zonas perturbadas pelo movimento da corda, sendo estas perturbações propagadas ao longo do espaço em todas as direções. Na pratica, o movimento oscilatório da corda repete-se durante um determinado período de tempo, acabando por se amortecer progressivamente devido ao atrito exercido pelo ar (fig. 3.2).
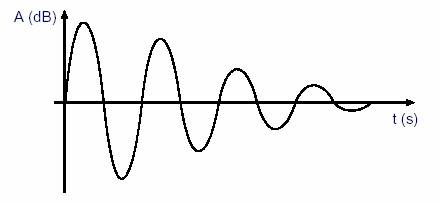
figura 3.1.2: movimento oscilatório amortecido
Para efeitos de análise, vamos admitir que este efeito de amortecimento não se manifesta, tal como aconteceria dentro de um ambiente vazio (em vácuo), e que o movimento oscilatório se repete indefinidamente mantendo constantes as amplitudes máximas e mínimas ao longo do tempo, como é ilustrado na figura 3:
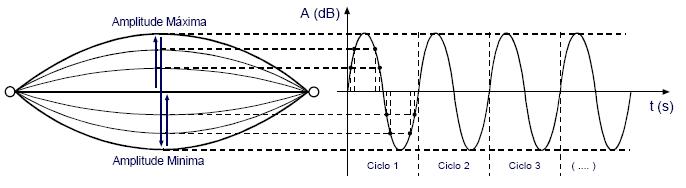
fig. 3.1.3
3.2. Principais grandezas associadas a uma forma de onda periódica
A uma forma de onda com um comportamento oscilatório periódico (que se repete ao longo do tempo segundo um padrão constante) tal como a sinusóide, é possível associar algumas grandezas básicas que estão diretamente relacionadas com características sonoras.
A amplitude quantifica a intensidade com que percepcionamos o som. A variação da amplitude é proporcional à variação da pressão atmosférica causada pela onda sonora. A unidade universal de medida da amplitude é o decibel (dB). A 0 dB corresponde o limiar de audição e a 130 dB corresponde o limiar da dor.
A freqüência traduz o número de ciclos por unidade de tempo numa forma de onda periódica e é uma das grandezas mais relevantes na caracterização de som. A unidade de medida universal da freqüência é o Hertz(Hz), que traduz o número de ciclos por segundo. O valor da freqüência de uma forma de onda periódica pode variar desde 0 Hz (forma de onda não oscilatória) até um valor virtualmente infinito. Na figura 4 são apresentados dois exemplos de ondas periódicas sinusoidais em que o número de ciclos por segundo é, respectivamente, 3 e 10, pelo que as suas freqüências serão de 3Hz e 10Hz.
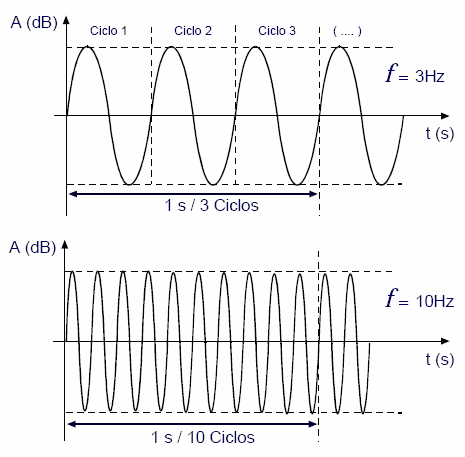
fig. 3.2.1
O ouvido humano percepciona ondas sonoras com freqüências compreendidas entre os 20Hz (graves) e os 20000 Hz (agudos). Contudo, as freqüências abaixo dos 20 Hz (infra-sons) e acima dos 20000 Hz (ultra-sons) são captadas pelo nosso corpo podendo provocar reações no cérebro, a nível do subliminar. A freqüência de uma onda é a grandeza que determina a altura tonal com que percepcionamos o som.
O período coincide com a noção de período de uma função e é, habitualmente, expresso em segundos (s). A freqüência f relaciona-se com o período p no sentido em que f = p-1.
O comprimento de onda corresponde ao comprimento de um ciclo da onda e é usualmente expresso em metros (m). O comprimento c de onda está diretamente relacionado com a freqüência f, uma vez que a velocidade v de propagação da onda é dada por v = cf. A freqüência é inversamente proporcional ao comprimento de onda, pois assume-se que a velocidade de propagação de uma determinada onda é constante.
A fase de uma onda resulta da associação de um ciclo da onda com uma volta na circunferência, sendo expressa em graus. Graficamente, a amplitude de uma onda pode ser representada em função da fase:
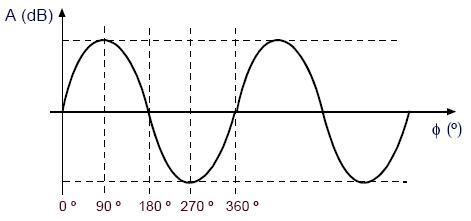
fig. 3.2.2: amplitude da onda em função da fase
A fase de um sinal é aparentemente insignificante, do ponto de vista perceptivo, pois dois sons que diferem apenas na sua fase inicial, dificilmente são distinguidos pelo ouvido humano. No entanto se considerarmos, por exemplo, a audição simultânea de duas sinusóides defasadas de 180º com amplitudes e freqüências idênticas, o resultado da soma dos dois sinais será um sinal de amplitude nula, ou seja o silêncio.
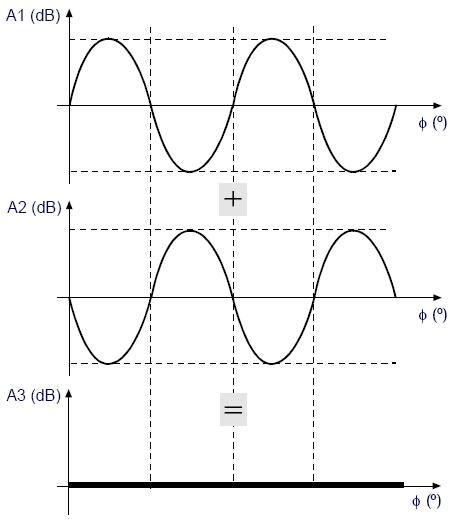
fig. 3.2.3: oposição de fase
A anulação ou redução de componentes de som por adição do próprio sinal em oposição de fase tem grande aplicação prática, já existindo produtos comerciais baseados neste conceito, tais como anuladores de ruído para aviões e carros integrados nos sistemas de som.
3.3. Representações gráficas do som: domínio temporal e domínio espectral
O som pode ser representado graficamente como a variação de amplitude da pressão, produzida pelo movimento das moléculas de um certo ponto do espaço, num determinado intervalo de tempo. A partir desta representação, podemos então analisar algumas características do som, como a freqüência e a amplitude. Esta forma de representação do som, que foi a utilizada até agora, denomina-se por domínio temporal.
Os domínios temporais até agora exemplificados são representados por ondas sinusoidais (à exceção da fig. 3.1.2). Contudo, estas representações estão defasadas da realidade, pois qualquer som do mundo real, mesmo que supostamente periódico, nunca pode ser representado com tanta simplicidade [1].
No domínio temporal do som da corda de guitarra exemplificado na figura 3, apenas foi contemplado o movimento oscilatório principal, o qual está associado à freqüência fundamental da corda – a que mais caracteriza a tonalidade do som. Um som deste tipo, composto apenas por uma freqüência, chama-se som puro. Os sons puros não existem no mundo real, embora possam ser gerados por processos eletrônicos. Contudo, há sons reais que são quase sons puros, como é o caso do som emitido por um diapasão. O som duma corda de guitarra, é composto por um leque de sons puros – harmônicos – hierarquizados pelas respectivas amplitudes. O harmônico correspondente à freqüência fundamental é o mais influente na tonalidade do som, pois é o que tem maior amplitude; os harmônicos associados aos movimentos oscilatórios secundários, têm tendência a possuírem menores amplitudes, à medida que as suas freqüências se distanciam da freqüência principal.
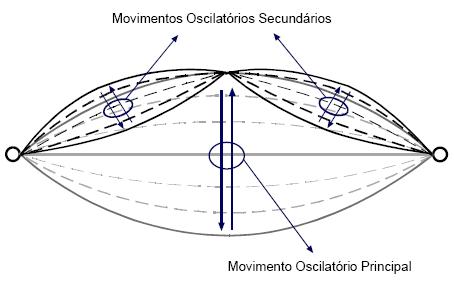
fig. 3.3.1: movimentos oscilatórios manifestados na vibração de uma corda
O timbre de um som é determinado pelos seus harmônicos e pelas amplitudes relativas com que estes se manifestam no som. O timbre é a característica sonora que nos permite distinguir duas notas com a mesma altura tonal provenientes de dois instrumentos diferentes.
Ao timbre está associado outra forma de representação gráfica do som que é o domínio espectral ou espectro. O espectro dum som consiste na representação da amplitude máxima, pico de amplitude, para cada freqüência que faz parte da composição do som, num intervalo de tempo. Este tipo de representação ajuda-nos a compreender o timbre de um som porque ilustra as amplitudes dos harmônicos que intervêm na sua composição. O espectro é uma espécie de fotografia do som. O espectro dos sons puros, porque compostos apenas por uma freqüência, consiste apenas numa barra vertical, de altura proporcional à sua amplitude de pressão. A figura 7 mostra o espectro do som gerado por uma sinusoidal com freqüência de 440 Hz:
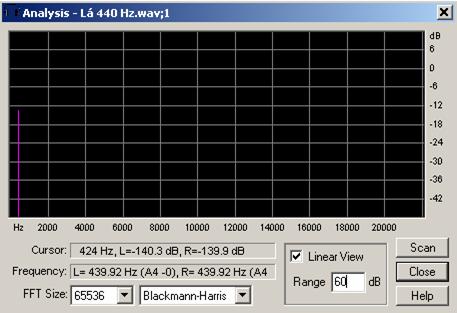
fig. 3.3.2: espectro de uma onda sinusoidal
A figura 8 mostra o espectro de um som real:
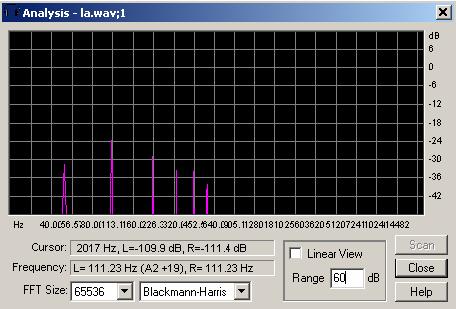
fig. 3.3.3: espectro do som da corda de uma guitarra elétrica
As representações gráficas do som baseiam-se geralmente no domínio temporal e espectral, sendo possível também representar simultaneamente os dois domínios:
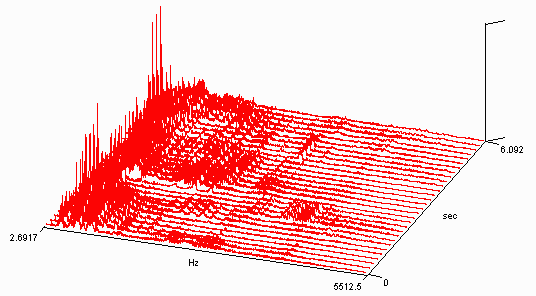
fig. 3.3.4: representação simultânea do domínio temporal e do espectro de um som
3.4. Consonâncias
Quando uma corda de guitarra vibra livremente, desencadeia-se uma série de oscilações de diferentes freqüências e amplitudes – harmônicos – que compõem o som.
A freqüência 
de cada harmônico n presente no som, é dada por 
, em que l é o comprimento da corda, T a tensão a que a corda está sujeita e 
a densidade linear da corda. Esta fórmula permite observar que todas as freqüências são múltiplas da freqüência fundamental 
, pelo que a freqüência do harmônico n é dada por 
.
O som que está a uma distância de um intervalo de oitava do som da corda solta, obtém-se se fizermos vibrar livremente metade da corda. As diversas freqüências podem ser obtidas usando a fórmula acima: a tensão e densidade linear mantêm-se, alterando-se apenas o comprimento, que passa a ser l/2. Assim, a freqüência 
de cada harmônico n deste novo som passa a ser 
.
Daqui observa-se que todos os harmônicos deste som correspondem aos harmônicos de índice par do som inicial (do ponto de vista das freqüências, que é o fator relevante para as relações entre sons). Esta é a razão porque o ouvido humano sente que dois sons relacionados por um intervalo de oitava estão fortemente relacionados, parecendo de certo modo que são idênticos (dois sons nestas circunstâncias representam a mesma nota musical).
O intervalo de quinta perfeita obtém-se por intermédio dos sons da corda solta e de duas terças partes. A freqüência 
do harmônico n presente na nova divisão da corda é 
. Assim, 
, ou seja, os harmônicos de índice par deste novo som correspondem aos harmônicos com índice múltiplo de três do som inicial. O intervalo de quarta perfeita pode ser obtido através dos sons da corda solta e de três quartas partes da corda. A freqüência 
do harmônico n deste som é dada por 
. Os harmônicos 3n do novo som coincidem com os harmônicos 4n do som inicial.
Estes intervalos representam as consonâncias mais importantes, não só pelo que aqui foi constatado, mas mais até pela relevância que lhes tem sido atribuída ao longo dos tempos e dos lugares – estes intervalos foram usados por praticamente todas as culturas, antes mesmo dos gregos terem descoberto a aritmética pela qual estes se regem. A diversidade de interpretações que pode ser dada a estes intervalos pode ser constatada, por exemplo, quando ouvimos um twelve bar Blues, ou quando presenciamos um popular cantar ao desafio.
3.5. Análise e síntese de som
A decomposição de um som periódico qualquer nos seus sons puros, representados por sinusóides, é o processo que permite transformar a representação temporal do som no seu espectro. A ferramenta matemática que sustenta todo este processo é as Séries de Fourier. As Séries de Fourier permitem que uma função periódica f(t) de período 2l, sob determinadas condições, possa ser expressa como uma soma infinita de senos e cossenos [2]:
, em que 
.
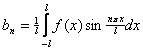
Assim, se f(t) representar a amplitude de um som periódico, em função do tempo, então este é composto por (ou pode ser decomposto em) uma série infinita de ondas sinusoidais – harmônicos – com freqüências múltiplas inteiras da freqüência fundamental, cada uma com uma determinada amplitude e uma determinada fase, mais uma componente contínua (de freqüência zero).
Uma das aplicações mais importantes da decomposição de uma onda sonora nas suas componentes elementares é a síntese de som. A síntese de som consiste em construir uma função a partir da soma de um número finito de parcelas do desenvolvimento em série de Fourier do som f(t) e, por processos eletrônicos, reproduzir o som associado a essa função. A síntese permite construir um som aproximado do som f(t) se a função construída for a série de Fourier truncada mas com um número suficientemente grande de parcelas.
3.6. Sintetizar o som da corda de uma guitarra
Uma forma de sintetizar um som concreto é começar por ter acesso ao seu domínio temporal. Os domínios temporais abaixo representados correspondem ao som f(t) de uma corda de guitarra elétrica afinada em lá2 220 Hz:
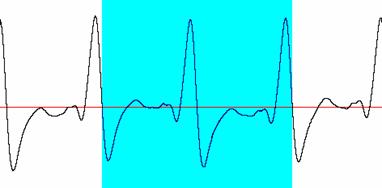
fig. 3.5.1
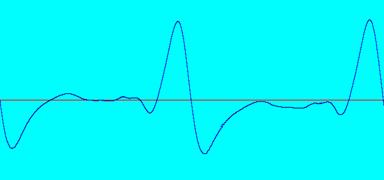
fig. 3.5.2: zoom da zona colorida da fig. 3.5.1
A figura 11 ilustra um ciclo do som da corda da guitarra, ao qual está associado o período P, que corresponde à duração em segundos. Com um programa adequado é possível interpolar o gráfico da função e obter assim uma expressão analítica g(t) que aproxima a função. Conhecendo-se g(t) é então possível obter o seu desenvolvimento em série de Fourier, que fornece a informação acerca das sinusoidais que compõe g(t). Como as ondas sinusoidais são facilmente geradas por computador, tomam-se as primeiras n sinusoidais de g(t), para n suficientemente grande, e introduz-se num sintetizador, que as reproduz através dos seus osciladores de freqüência.
3.7. Som digital
Em 1957, Max Mathews realizou a primeira gravação digital e a primeira síntese de sons por computador. O processo consiste em representar a onda f(t) por uma seqüência discreta de números que representam os valores sucessivos de f(t) em intervalos de tempo bastante próximos. A amostragem é o processo que se utiliza para obter a seqüência que representa a onda f(t).
O microfone é a ferramenta que transforma essas variações em impulsos elétricos v(t), de forma linear. Assim, o comportamento de v(t) é equiparável ao comportamento de f(t). A gravação consiste no registro do valor do sinal v(t) em vários instantes de tempo, sendo estes valores gravados num arquivo que podemos por exemplo manipular num computador. A gravação vai necessariamente estar dependente de dois parâmetros:
Freqüência de amostragem F – corresponde ao número de registros do sinal v(t) por segundo. A freqüência de amostragem está relacionada com o período de amostragem pois F=P-1.
Quantificação Q – pode ser encarada como a precisão que vai ser utilizada para medir o valor do sinal v(t). A quantificação é expressa em bits, sendo de 16 bits numa gravação de CD áudio. Uma gravação de 16 bits permite 216 = 65536 níveis de discriminação de valores do sinal v(t).
A qualidade de gravação está diretamente relacionada com os valores destes parâmetros. A freqüência de amostragem constitui mesmo um fator de integridade do som: para que um som real (analógico) depois de digitalizado possa ser novamente reproduzido mantendo as suas características essenciais preservadas, tem-se que garantir que a freqüência da amostragem utilizada seja pelo menos o dobro da maior freqüência que intervém na composição do som. A freqüência de amostragem utilizada nos discos compactos é de 44100 Hz. Este valor de freqüência foi determinado em 1947 por Claude Shannon na sua teoria matemática sobre comunicação, que garante que as freqüências até os 22050 Hz sejam preservadas, o que é suficiente pois o ouvido humano não reconhece as freqüências superiores a 20000 Hz.
A reprodução é o processo que transforma a seqüência de números binários em variações da pressão atmosférica, ou seja, som. A freqüência com que os números são devolvidos à atmosfera tem que ser a mesma com que eles foram registrados.
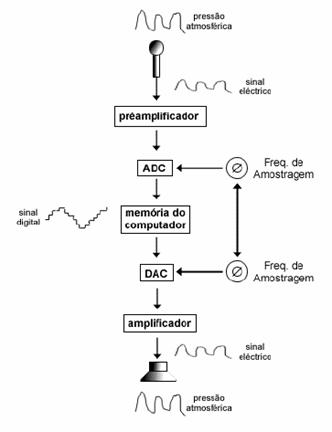
figura 12: processo de gravação digital e de reprodução de um formato digital
Notas:
[1] Esta questão é abordada no Apêndice
[2] Demonstrado no Apêndice.