Matemática na Música – Anexo
Séries de Fourier
Seja g(t) uma função periódica de período ![]() , definida em IR e integrável, segundo Riemann, em qualquer intervalo limitado. O nosso pressuposto é averiguar se g pode ser ‘expandida’ numa série da forma
, definida em IR e integrável, segundo Riemann, em qualquer intervalo limitado. O nosso pressuposto é averiguar se g pode ser ‘expandida’ numa série da forma ![]() . (1)
. (1)
Na fórmula acima, ![]() é o coeficiente correspondente à função constante
é o coeficiente correspondente à função constante ![]() , em que o fator
, em que o fator ![]() está presente por conveniência. O termo
está presente por conveniência. O termo ![]() não aparece pois
não aparece pois ![]() . Tendo em conta que
. Tendo em conta que ![]() e que
e que ![]() , a equação (1) pode ser rescrita na forma
, a equação (1) pode ser rescrita na forma ![]() (2) com
(2) com ![]()
![]() e
e ![]() , para cada
, para cada ![]() . Para o que se segue, iremos explorar principalmente (2), contudo devemos também associar os resultados a (1).
. Para o que se segue, iremos explorar principalmente (2), contudo devemos também associar os resultados a (1).
Admitindo então a igualdade (2), impõe-se-nos determinar os coeficientes ![]() , que dependerão de g. Se multiplicarmos ambos os membros de (2) por
, que dependerão de g. Se multiplicarmos ambos os membros de (2) por ![]() , com k inteiro, e integrarmos de
, com k inteiro, e integrarmos de ![]() a
a ![]() , resulta que
, resulta que 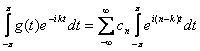 .
.
Como 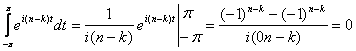 , para
, para ![]() , e
, e 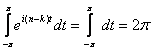 para
para ![]() , resulta então que o único termo que sobrevive após a integração é o termo em que
, resulta então que o único termo que sobrevive após a integração é o termo em que ![]() , donde se obtém
, donde se obtém 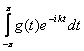 =
= ![]() , para k inteiro.
, para k inteiro.
Trocando k por n, obtém-se a fórmula desejada para os coeficientes de ![]() :
: 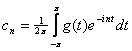 , (3) tornando-se agora simples a determinação dos coeficientes
, (3) tornando-se agora simples a determinação dos coeficientes ![]() e
e ![]() da expressão (1), pois:
da expressão (1), pois:
![]()
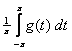 ,
,
![]()
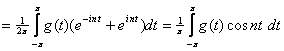 , para
, para ![]()
![]()
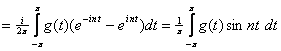 , para
, para ![]() .
.
Os números ![]() ou os números
ou os números ![]()
![]() denominam-se por coeficientes de Fourier, os quais estão associados às respectivas fórmulas (1) e (2), denominadas por séries de Fourier. Para nos convencermos mais seriamente que efetivamente g(t) pode ser ‘expandida’ como uma série de senos e cossenos, seria ainda necessário constatar que a série realmente converge para a função g, o que não será mostrado aqui.
denominam-se por coeficientes de Fourier, os quais estão associados às respectivas fórmulas (1) e (2), denominadas por séries de Fourier. Para nos convencermos mais seriamente que efetivamente g(t) pode ser ‘expandida’ como uma série de senos e cossenos, seria ainda necessário constatar que a série realmente converge para a função g, o que não será mostrado aqui.
A ideia de expandir uma função como série de senos e cossenos pode ser agora facilmente generalizada a qualquer função periódica e integrável segundo Riemann:
Seja f(x) uma função periódica de período ![]() , e considere-se a seguinte mudança de variáveis
, e considere-se a seguinte mudança de variáveis ![]() ,
, ![]() .
.
Com esta mudança de variáveis resulta que g(t) é uma função periódica e, tal como f(x), satisfaz a condição de Riemann, pelo que pode ser expandida na forma de (2). Substituindo em (2) e em (3) a variável t por ![]() (note-se que
(note-se que ![]() e
e ![]() ), resulta então que
), resulta então que ![]() com
com 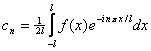 .
.
A série de senos e cossenos correspondente é ![]() , com
, com ![]()
 (
(![]() ) e
) e 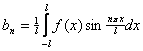 (
(![]() ).
).







