Tem Música No Triângulo de Pitágoras
por: Prof.Luiz Netto

O sábio matemático Bernardus Vallumbrosius, certamente que ao contemplar os valores constituintes da Escala Musical Temperada, notou algumas valôres que lhe pareceram bem familiares como 1,4142 = Raiz Quadrada de 2, – o valor 0,7071 = Raiz Quadrade de 2/2 – (que aparece como uma distância de corda) – e imediatamente se lembrou do Triângulo Retângulo, com dois lados iguais, onde estes valôres aparecem.
Intrigado com isso resolveu construir triângulos retângulos cujas hipotenusas tivessem uma sequência constituida pelos números que representam os sucessivos intervalos e viu que os catetos poderiam ser representados também na base 2 elevado à 1/12. De modo que construiu então os triângulos que são representados abaixo.
E exclamou: Eureka!: Descobri queTem Música No Triângulo Retângulo! Ainda bem que eu achei seus alfarrábios e pude reproduzí-los aqui.
Em homenagem ao matemático Bernardus Vallumbrosius, denominei-os Triângulos Vallumbrosianos.

Do 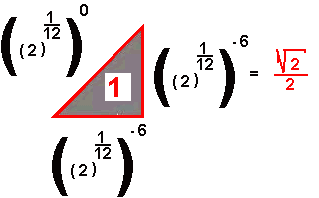 |
Do#  |
Re 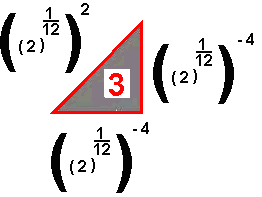 |
Re# 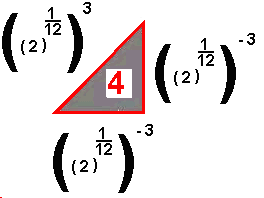 |
Mi 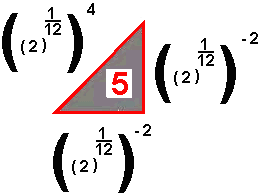 |
Fa 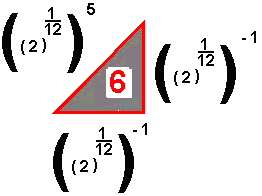
|
Fa# 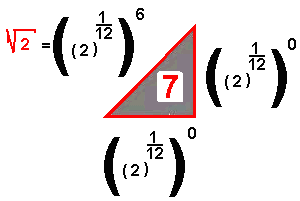 |
Sol 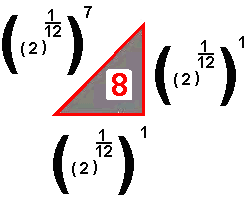 |
Sol# 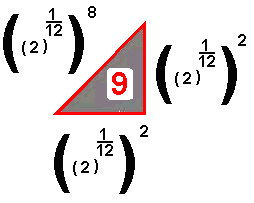 |
La 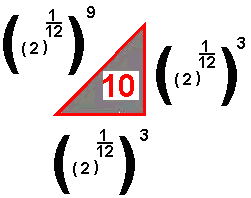
|
La# 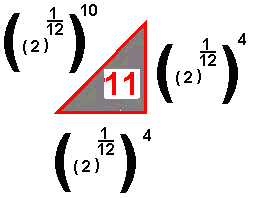 |
Si 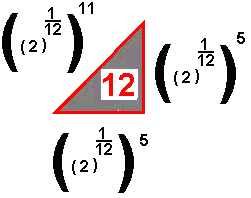 |
Do2 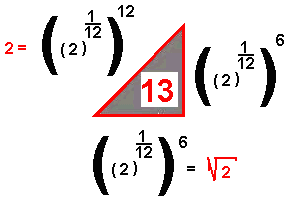 |
O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil







