Uma Progressão Geométrica Muito Especial

por: Prof.Luiz Netto

Quando no estudo da matemática nos deparamos com algum tópico que podemos visualizar uma aplicação prática, e para nossa felicidade, há muitos deles, se já apreciamos o seu estudo, isto reforça ainda mais nosso interesse, pois afinal aquilo que é produto exclusivo da inteligência do homem, a matemática, encontra um modelo prático que represente o que era produto da inteligência, da imaginação. Assim, quando estudamos a matemática da música, em seus vários aspectos, como por exemplo, na análise das sequências das notas sonoras da escala musical igualmente temperada, nos damos conta que os valores das frequências das sequências de notas de uma oitava, formam uma PROGRESSÃO GEOMÉTRICA, cuja razão é igual a dois elevado a um doze avos.

Eu teria gostado muitíssimo em minha época de estudante que meus professores me houvessem chamado atenção para este fato, para essa progressão especial, que fala de algo que não há ser humano que não goste: A Música. Assim, além de descobrir algo novo, teria aumentado ainda mais o meu interesse pelo seu estudo. Mas… as vezes acho que poucos deles sabiam disso… porque claro está que na medida que mostramos as múltiplas utilidades dos estudos de matemática, aumenta o interesse do aluno e deixaríamos de ouvir de muitos estudantes: Não gosto de matemática… ! – quando na verdade estão expressando que não gostam é daquilo que não compreendem e comprender certas coisas – depende muito da didática daqueles que nos ensinam! Mas, deixemos um pouco de lado dessa filosofia pedagógica, e voltemos para a nossa progressão geométrica.

Assim, podemos imaginar essa progressão geométrica com o primeiro termo igual a unidade, e os termos subsequentes obtidos atraves das multiplicações sucessivas por 1,0594631:

Vemos aqui uma sequência de 13 têrmos dessa progressão geométrica que representa a sequência das notas da escala musical igualmente temperada pois 12 são seus intervalos musicais compondo uma oitava. O número 2, sobre o número 1,0594631 corresponde ao primeiro intervalo. O décimo terceiro termo já pertence à próxima oitava, ou seja se você começa por exemplo pela nota do – (1), quando tiver subido uma oitava, a frequência dessa nota será o dobro – (2). Assim, se a nota escolhida for a nota LA2, que sabemos tem uma frequência de 220 Hz, quando tivermos percorrido a oitava toda, a frequência será de 440 Hz.

Exemplificando, para a nota La2: É só multiplicarmos todos estes números da sequência da PG por 220: 220*1 – 220*1.0594631 – 220*1,1224621 e teremos a sequência:

Assim, você percebe que pode escolher qualquer um destes números e ir multiplicando sequencialmente pela razão 1,0594631 para obter todas as notas das oitavas seguintes, ou seja todos os termos dessa progressão geométrica, muito especial, porque com ela construímos a Escala Musical Igualmente Temperada.

OUTRA PROGRESSÃO GEOMÉTRICA MUITO ESPECIAL

O leitor poderá indagar o que poderia representar uma progressão geométrica cujos termos fossem formados pelo inverso dessa razão, ou seja: 1/(1.0594631)^n, ou seja o primeiro termo como 1 e os outros obtidos pela multipicação por essa razão. Então teríamos para o primeiro termo, o inverso de 1 que é um mesmo, para o segundo termo,

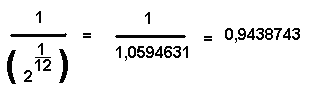
para o terceiro termo o inverso de 1,1224621, para o quarto termo, o inverso de 1,189 2071, e assim sucessivamente, formando a seguinte sequência de têrmos:

1 – 0,9438743 – 0,8908987 – 0,8408964 – 0,7937005 – 0,7491535 – 0,7071067 – 0,6674198 – 0,6299604 – 0,5946035 – 0,5612309 – 0,5297314 – 0,5….. etc…

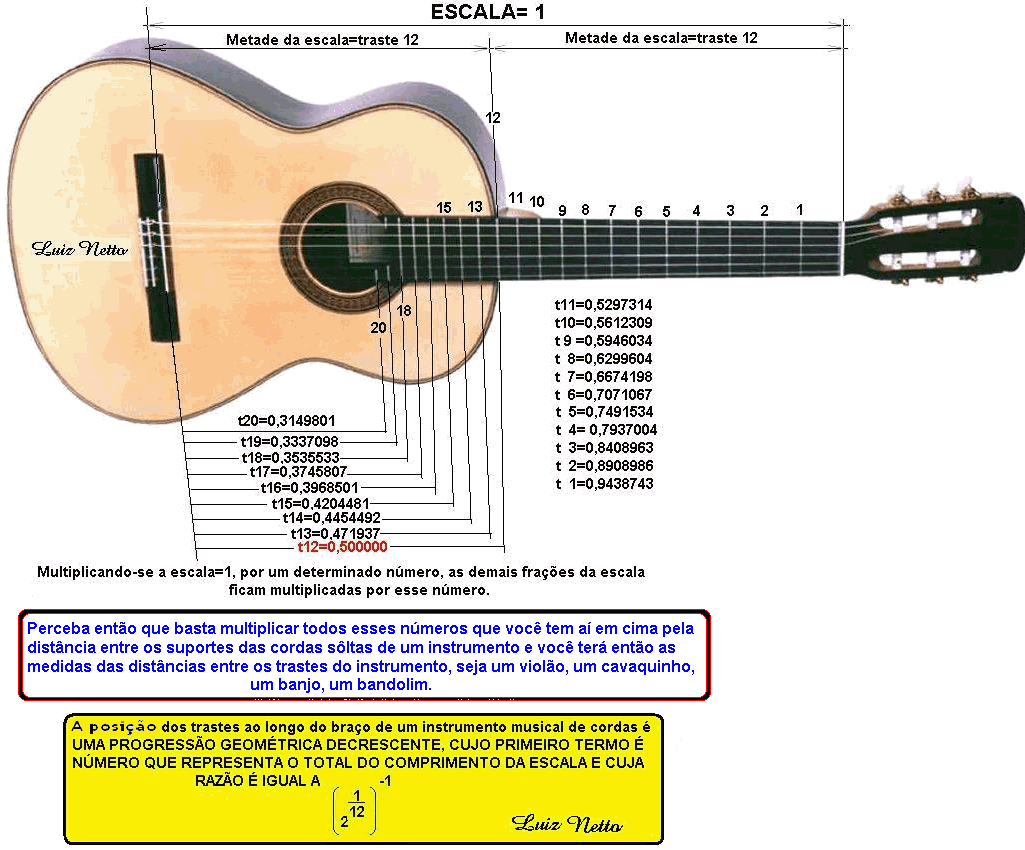
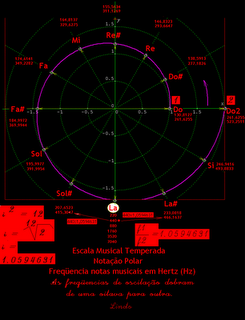
Mas o que esta sequência de números podem representar? – Estas sequências de números podem representar os comprimentos das cordas que percurtimos para obter as várias frequências da progressão geométrica de razão 1.0594631. Vejam a figura abaixo, o instrumento violão, onde aparecem todos esses números. Você pode escolher então como primeiro termo de sua progressão geométrica, inversa daquela primeira que estudamos, como sendo o comprimento das distâncias entre as cordas soltas do instrumento e assim obterá todas as distancias das cordas que correspondem as frequências obtidas, multiplicando seguinda pela razão: 0,9438743. Não é mesmo espetacular? …Hein? Então, a matemática é algo para ser estudado com muito carinho, devagar, sem pressa, com reflexão, porque uma vez entendido algo, e bem entendido, esse entendimento traz uma grande satisfação interior, qual seja; O SABER, e uma outra maior ainda, poder ensinar aquilo que foi entendido.

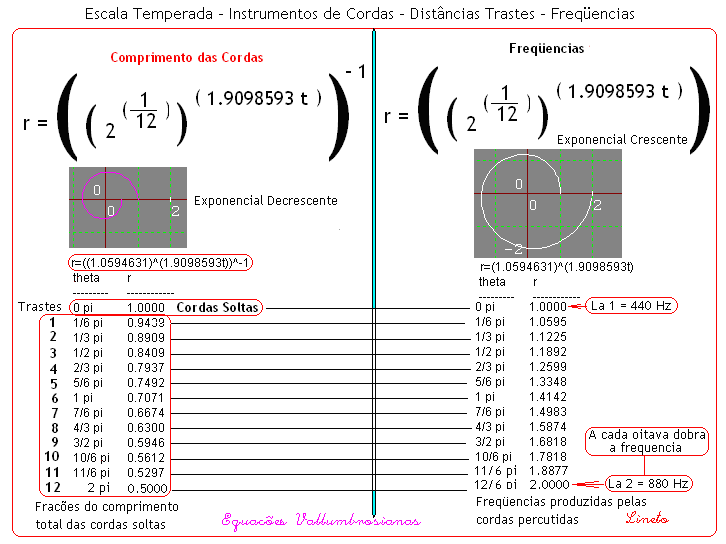
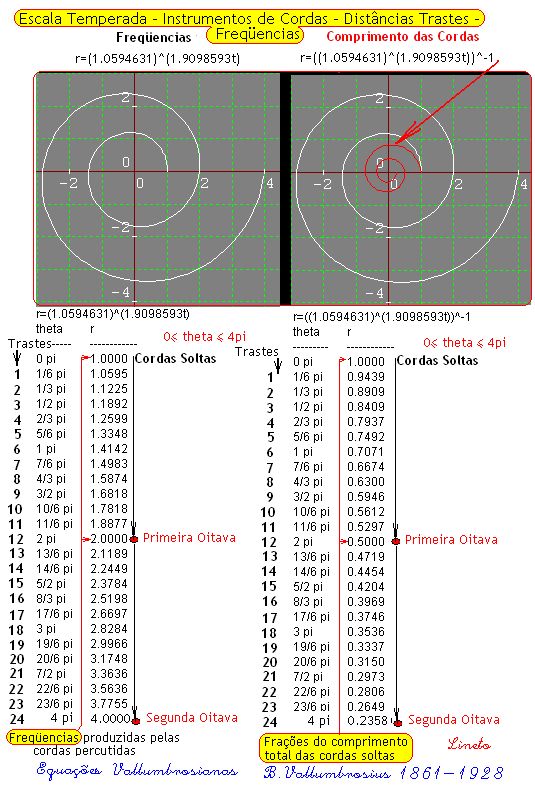
À Circunferência mais externa do lado das frequências, corresponde a circunferência mais interna do lado do Comprimento das Cordas – Quanto mais alta é a frequência menor é o comprimento da corda que produz sua vibração. Repare que embora os invervalos sejam iguais, eles vão ocupando espaços cada vez maiores do lado das frequências e o inverso ocorre do lado do comprimento das cordas.

Obras Consultadas:
Equações Vallumbrosianas
Bernardus Vallumbrosius 1861-1928

O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil

Retornar ao Índice