A Escala Musical Temperada e os Juros Compostos
por: Prof.Luiz Netto
É curioso notar que as frequencias das notas musicais na escala musical temperada tem um comportamento de crescimento semelhante ao cálculo de juros compostos. É só considerarmos que na escala musical temperada de 12 intervalos a taxa de crescimento é de 5,94631%).

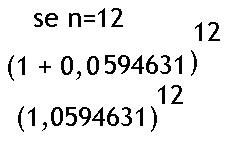

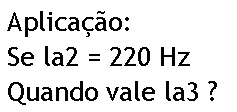
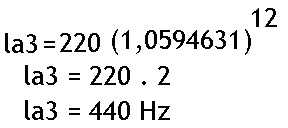
Aplicando esta fórmula você pode calcular todos os valores das notas musicais da escala musical temperada de meio em meio tom, é só ir variando o expoente de zero à 12, partindo da frequencia de uma nota musical conhecida. O intervalo entre as duas notas aqui calculadas é de uma oitava porque o quociente entre elas é 2.
Veja o quadro abaixo:
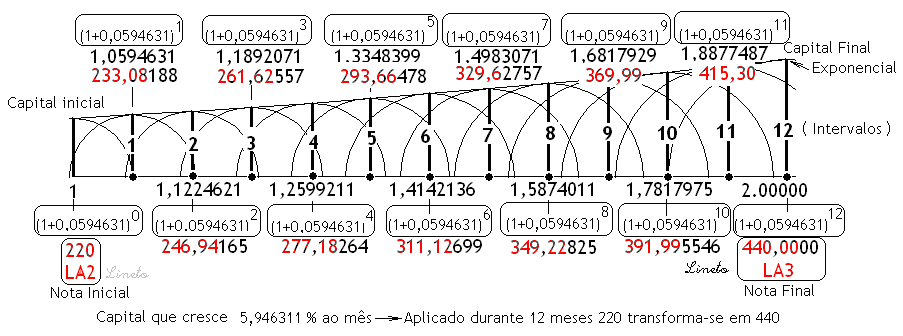
Se a nota musical inicial é 220 Hz, (LA2) – teremos:
la#2 = 233,08 Hz,
si2 = 246,94 Hz,
do3 = 261,62 Hz,
do#3 = 277,18 Hz,
re3 =293,66 Hz,
re#3 = 311,12 Hz,
mi3 = 329,62 Hz,
fa3 = 349,22 Hz,
fa#3 = 369,99 Hz,
sol3 = 391,99 Hz,
sol#3 = 415,30 Hz,
LA3 = 440,00 Hz.
Veja então que a formula de cálculo é a mesma para as duas situações, quer estejamos a calcular o crescer das frequencias na escala musical, ou calculando juros compostos.
|
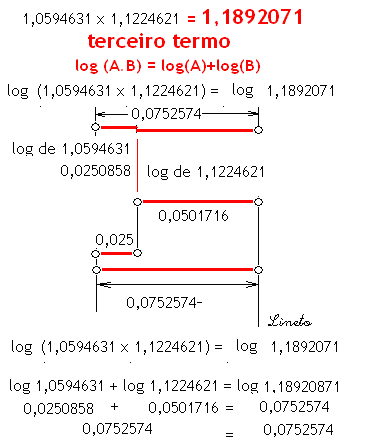
LOGARÍTMO DE UM PRODUTO Log (A.B) = Log A + Log B
|
O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil