Intervalos – O Ciclo de Quintas
por: Prof.Luiz Netto
Nota: Este estudo (Representação Polar da Escala Musical) é algo que não encontrei até hoje tanto em livros como na internet. Nunca encontrei esta equação que estou utilizando: r = (1.0594631)^(1.9098593t). (Notação utilizada nos programas de geração de gráficos).
 |
Encontrei algo sugerindo a ideia dessa espiral logarítmica para representar as oitavas musicais, mas que o autor não saberia qual a equação que poderia descrevê-la. Estudando-a, eu a desenvolvi. Claro está que a maneira tradicional de representação é uma maneira simbólica muito boa. – O que pretendemos é descrever matematicamente a sequencia de quintas e claro podemos fazer isto também com os intervalos de Quartas.
 |
| DO C | MI 3 E | SOL 5# G# |
| Do# | Fa3 | La5 |
| Re | Fa3# | La5# |
| Re# | Sol3 | Si5 |
| Mi | Sol3# | Do6 |
| Fa | La3 | Do6# |
| Fa# | La3# | Re6 |
| SOL G | SI 3 B | RE 6# D# |
| Sol# | Do4 | Mi6 |
| La | Do4# | Fa6 |
| La# | Re4 | Fa6# |
| Si | Re4# | Sol6 |
| Do2 | Mi4 | Sol6# |
| Do2# | Fa4 | La6 |
| RE 2 D | FA 4# F# | LA 6# A# |
| Re2# | Sol4 | Si6 |
| Mi2 | Sol4# | Do7 |
| Fa2 | La4 | Do7# |
| Fa2# | La4# | Re7 |
| Sol2 | Si4 | Re7# |
| Sol2# | Do5 | Mi7 |
| LA 2 A | Do 5# C# | FA 7 F |
| La2# | Re5 | Fa7# |
| Si2 | Re5# | Sol7 |
| Do3 | Mi5 | Sol7# |
| Do3# | Fa5 | La7 |
| Re3 | Fa5# | La7# |
| Re3# | Sol5 | Si7->D0 8 -> C |
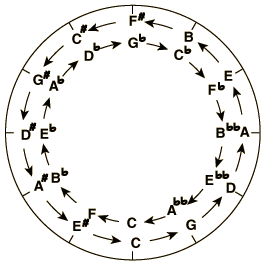
A maneira usual que se apresenta simbólicamente os intervalos de Quinta e de Quartas é utilizando uma circunferência com a sequencia de notas – C – G – D – A – E – B – F# – C# – G# – D# – A# – E# , para os intervalos de quintas como apresentado abaixo – e C – F – Bb – Eb – Ab – Db – Gb – Cb – Fb – Bbb – Ebb – Abb, para os intervalos de Quartas – O círculo interno. Podemos representar estas sequencias de um modo rigorosamente matemático. Vamos traçar os intervalos de quintas, utilizando a notação polar através da equação: r = n(1.0594631)^(1.9098593 t), com t medido em radianos e n com valores 2,4,8,16,32,64 – para traçar as espirais representativas dessas oitavas.
Modo usual de Representação dos Intervalos de Quintas e Quartas. A distância ângular entre as notas na sequencia de quintas é de 210 graus –(sobe 7 semitons -> 7*30 = 210 graus) – Isto é uma consequencia da adoção da divisão de uma oitava em 12 intervalos, o que no espaço de 360 graus, ou 2 pi radianos, equivale a distância de 30 graus, ou pi/6 radianos, entre os semitons. No sentido contrário aos ponteiros do relógio inicie pela nota C seguindo pelas notas – G – D – A – E (Este primeiro desenho). Na sequencia, no próximo desenho seguem-se as notas – B -C# – G# – D# – A# – E# – C – a partir daqui o ciclo se repete novamente. No intervalo de Quintas, são percorridos 7 oitavas para que as notas se repitam na mesma sequencia. REPRESENTAÇÃO DOS INTERVALOS DE QUINTAS ATRAVÉS DE NOTAÇÃO POLAR
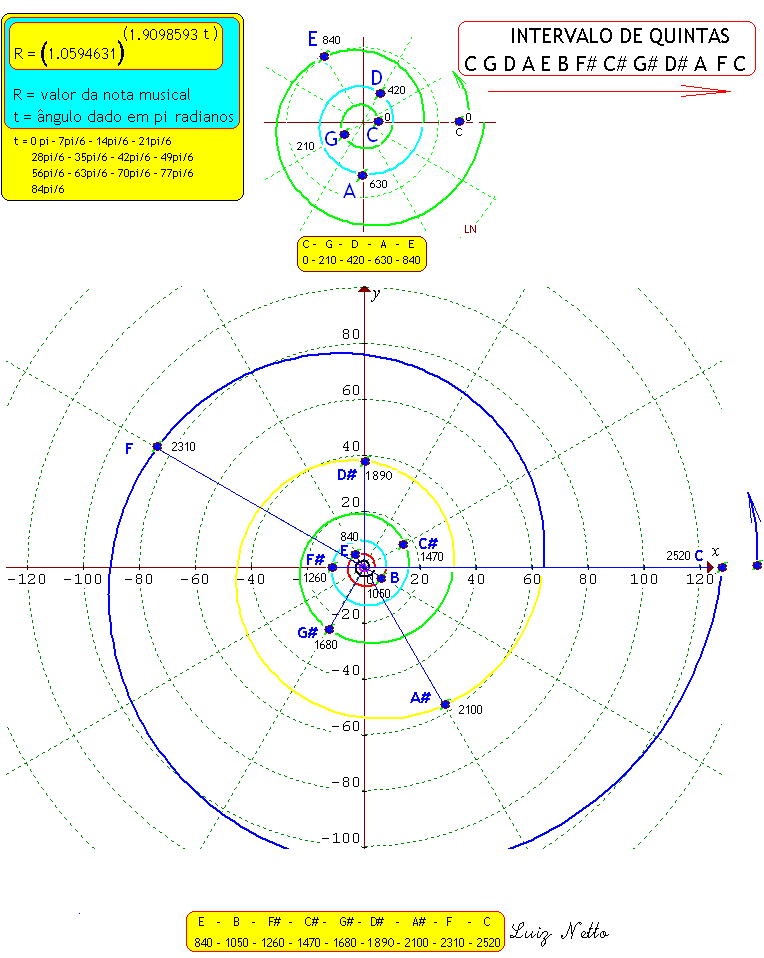
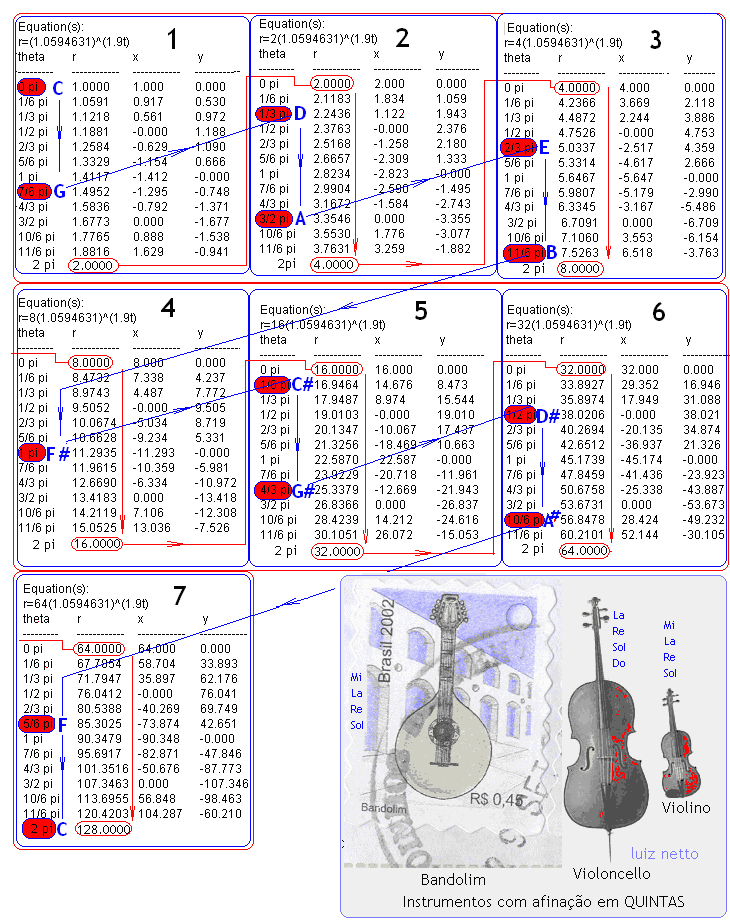
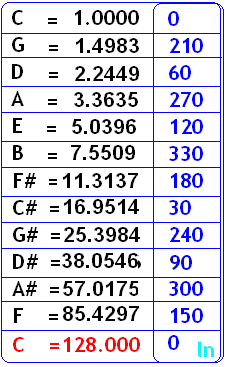
Representação do Intervalos de Quintas desde C até C– completando o ciclo das Quintas – Caminhe sobre a espiral – a partir de c até C – e veja os múltiplos de 30 graus entre uma nota e a seguinte – (7)x(30) = 210 graus.(Cada 30 graus eleva-se a frequencia da nota em 1 semiton.Estão representados os valores da nota e seu ângulo. CÁLCULO DOS VALORES DAS NOTAS NOS INTERVALOS DE QUINTAS Utilize um programa gráfico para traçar e plotar os valores de uma função. A função aqui é: r = n(1.0594631)^(1.9098593t), com os valores de n=1,2,4,8,16,32 e 64 e t variando de Zero a 2pi radianos.
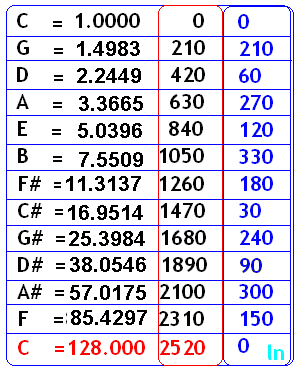
CICLO DE QUINTAS Nota Musical – ângulo Frequencia da nota Musical da sequencia de quintas e o seu ângulo correspondente
EXERCÍCIO Seja calcular o valor da última nota da sequencia de Quintas, a nota C: Sabemos que o ângulo é igual a 2520 graus, ou em radianos, é igual a (84*pi/6) radianos. A equação a ser aplicada é esta: (1.0594631)^(1.9098593*t). t aqui corresponde ao ângulo de (84*pi/6). Aplicando a equação vamos calcular o valor de C: valor do expoente –> (1.9098593*84*(3.1416/6)) = 84 então r= (1.0594631)^t = (1.0594631)^84 r = (1.0594631)^84 = 128 r=128 então: (1.0594631)^(1.9098593t)= 128
Problema Inverso Conhecendo-se o valor da nota, calcular qual o angulo (t) – (em radianos) que lhe corresponde.
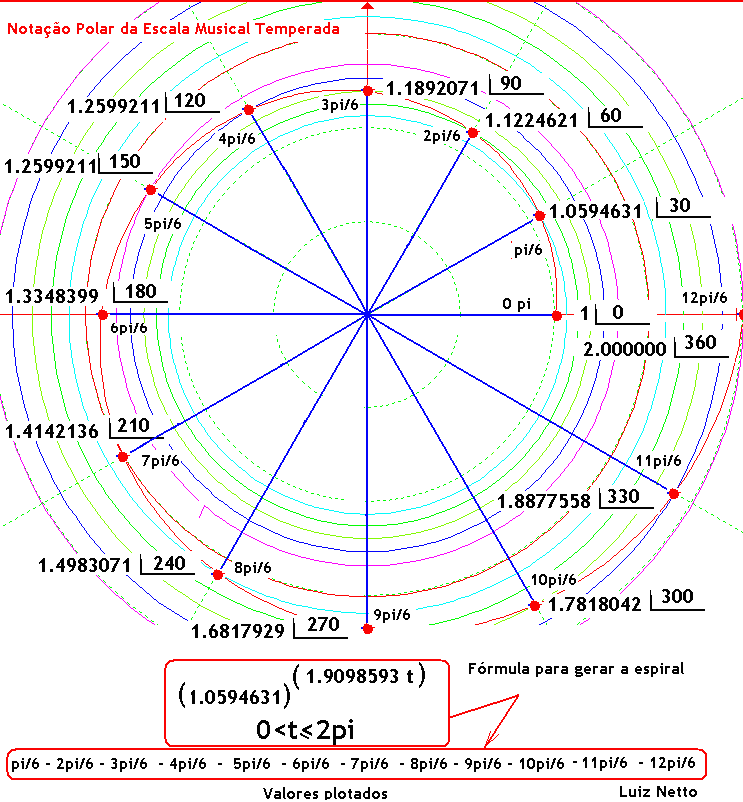
Notação Polar da Escala Musical Temperada – Representação de Uma Oitava
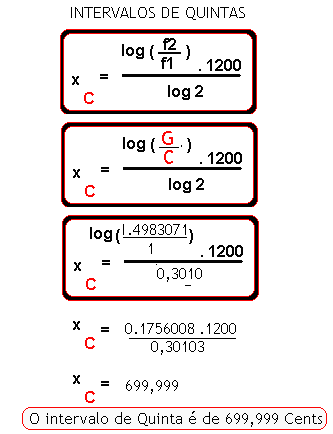
MEDIDA DE DO INTERVALO DE QUINTA
|
O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil