Características do Som – A Transformada de Fourier
por: Prof.Luiz Netto
São tres os parâmetros que definem um Som: A sua altura, ou seja a frequência, ou número de vibrações produzidas por segundo, a sua intensidade, ou o quanto forte ou quanto potente é o som, e o timbre, caracteristica esta que dá identidade a um instrumento, ou seja sabemos qual instrumento está emitindo um som.
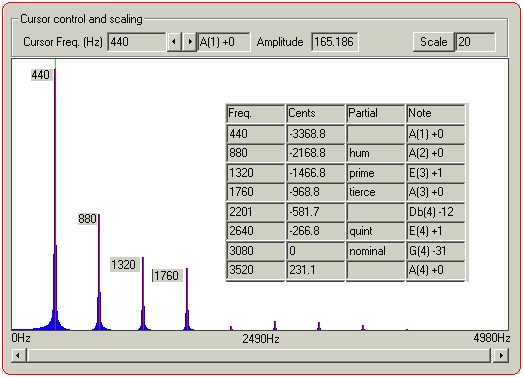
Quando vamos assistir a um concerto musical, podemos observar nos momentos que antecede a apresentação musical, os músicos afinando seus instrumentos; tomando por base a nota la3 = 440 Hz, ou ciclos por segundo – e se um violino e um piano emitem a mesma nota la3, embora a frequência seja a mesma sabemos identificar qual o som que vem do piano e qual o som que vem do violino.
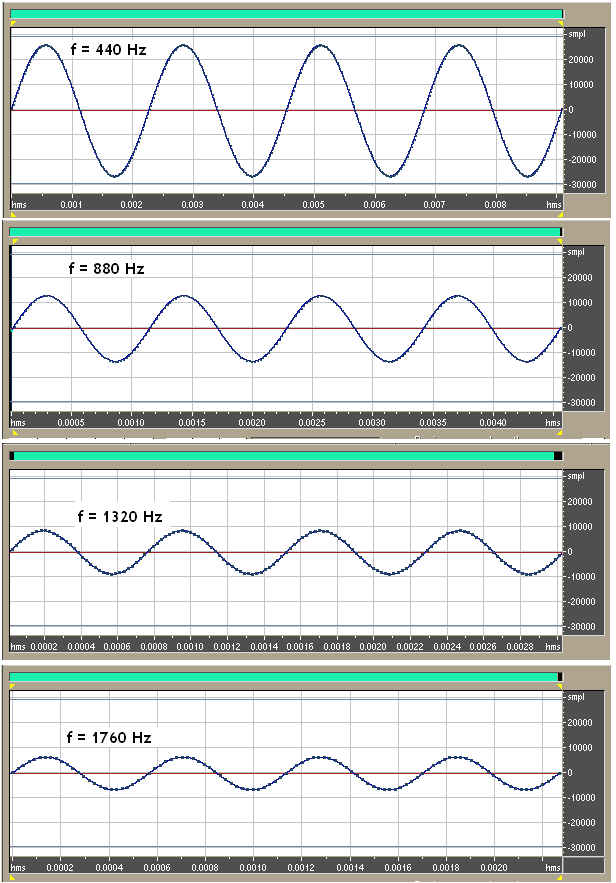
Por que? Porque o conteúdo harmônico desse som é diferente para um e para outro instrumento. Quando um instrumento gera um som, além da frequência fundamental, ele gera frequências superiores de ordem par e ordem ímpar em relação à fundamental, além do que os harmônicos são diferentes também na amplitude. Portanto a forma de onda desses instrumentos são diferentes e nosso ouvido percebe muito bem isso. Por esse mesmo motivo sabemos distinguir a voz de um interlocutor se é o individuo A, B, ou C.
É claro que esta é uma análise físico-matemática do som, mas certamente que o o músico, o maestro, o compositor, acrescentará uma outra característica fundamentalmente importante, que é a DURAÇÃO DO SOM, através das figuras de tempo, que impressas nas partituras, são o guia do músico, para transformar aqueles sinais gráficos que serão traduzidos em maravilhosos sons – permeados por PAUSAS, aqui e acolá, capazes de levar-nos a estados de alma de puro extase.
|
FOURIER Em meados do século XVII, o matemático francês J. Fourier provou matematicamente que qualquer forma de onda, independente da sua origem, é um somatório de ondas senoidais de diferentes frequências, amplitudes e fases. Ele mostrou que se a forma de onda se repete periodicamente, então as frequências das componentes senoidais são restritas a valores múltiplos da frequência de repetição da forma de onda. A transformada de Fourier representa a soma de uma série de formas de onda senoidais com diferentes amplitudes, fase e frequencia.
Observe o que Fourier descobriu: Qualquer sinal complexo pode ser decomposto em sinais senoidas, com fases e amplitudes determinadas.
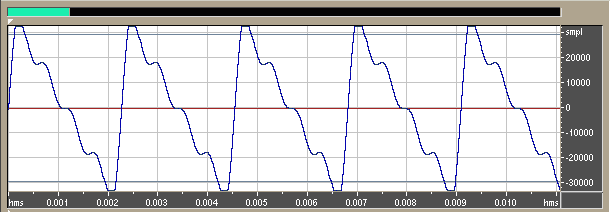
Se você colocar essa equação em um programa traçacador de gráficos de funções como por exemplo o da GRAPHMATICA (http://www.graphmatica.com/) poderá ver esta forma de onda. ONDA DENTE DE SERRA
Esta é a expressão matemática da forma de onda dente de serra acima ilustrada.
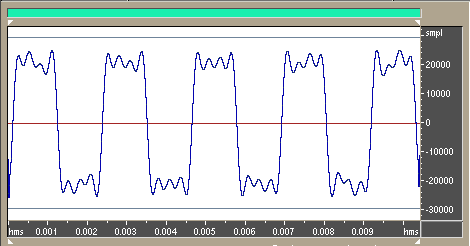
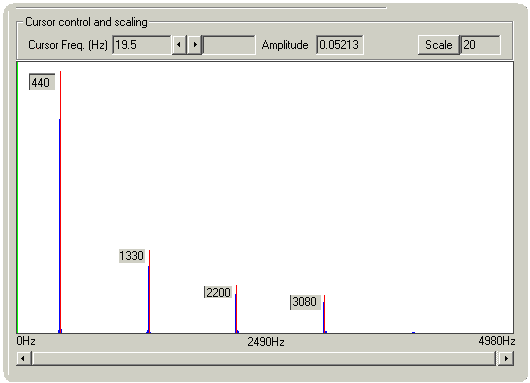
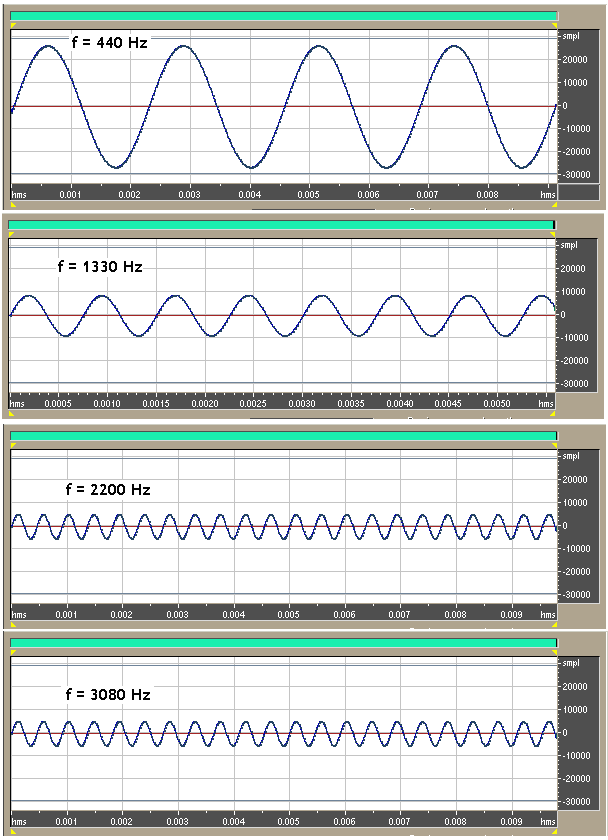
Análise do espectro de Frequências da Onda Dente de Serra, composto de (f,2f,3f,4f…, a fundamental mais os sinais de frequência de ordem par) COMPONENTES SENOIDAIS DA ONDA DENTE DE SERRA
A Soma Vetorial dessas ondas com essas frequências, com essas amplitudes e com essas fases, resultam na onda dente de serra mostrada acima.Quanto maior o número de componentes, mais perfeita fica a onda Dente de Serra. ONDA QUADRADA
Esta é a expressão matemática da forma de Onda Quadrada, acima ilustrada.
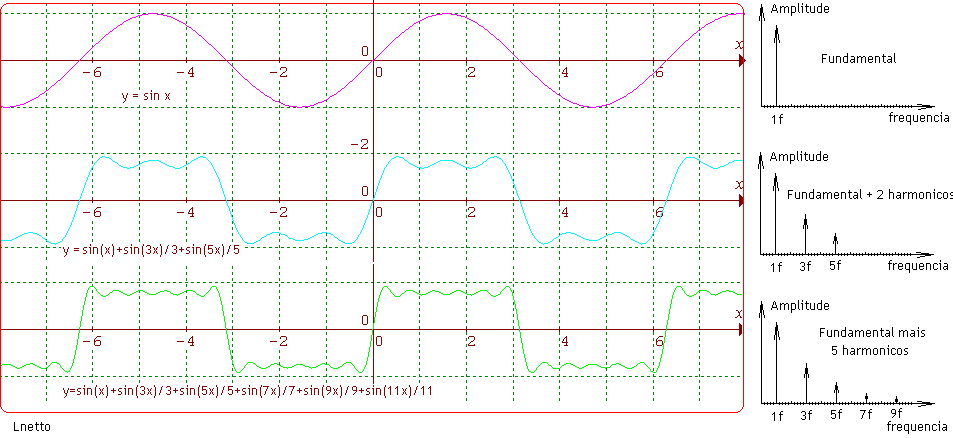
Análise do espectro de frequências da Onda Quadrada, composto de f,3f,5f,7f..(fundamental mais os sinais de frequência de ordem ímpar) COMPONENTES SENOIDAIS DA ONDA QUADRADA
A Soma Vetorial dessas ondas com essas frequências, com essas amplitudes e com essas fases, resultam na Onda Quadrada mostrada acima.Quanto maior o número de componentes mais perfeita fica a ONDA QUADRADA. |
O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil