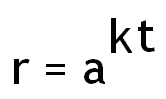Representação Espacial Tridimensional da Escala Musical Temperada

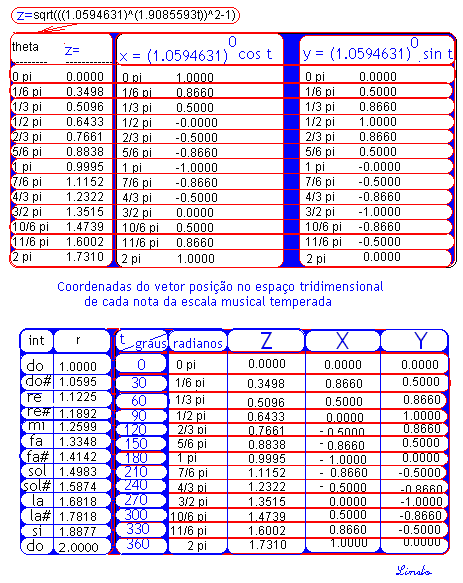
r = a^(kt)

Além da representação da escala musical temperada com seus vetores frequencia representados no espaço bidimensional, podemos fazer esta representação também no espaço tridimensional. Devo dizer que nunca vi isto deste modo, apenas proponho esta maneira de representá-la, como o fiz na representação polar em duas dimensões. Podemos imaginar os vetores girando em torno de um cilindro cujo raio da base tem o valor (1.0594631)^(1.9098593 t) para t = zero, com origens no centro do cilindro e cujas pontas percorram as paredes do cilindro subindo exponencialmente, de acordo com a equação (1.0594631)^(1.9098593 t).

A equação modelo é esta: r = a^kt, onde r = valor do intervalo musical na escala musical temperada; k é uma constante adotada para que todos os valores de uma oitava sejam mostrados no desenvolvimento de 2pi radianos; t é o ângulo associado ao valor de r; e a é igual a 1.0594631 – que é a raiz décima segunda de dois – dado que a equação fundamental da escala temperada é: i^12 = 2.

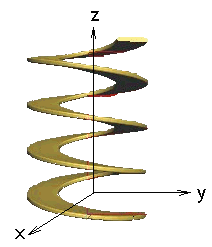
Representação espacial da escala musical

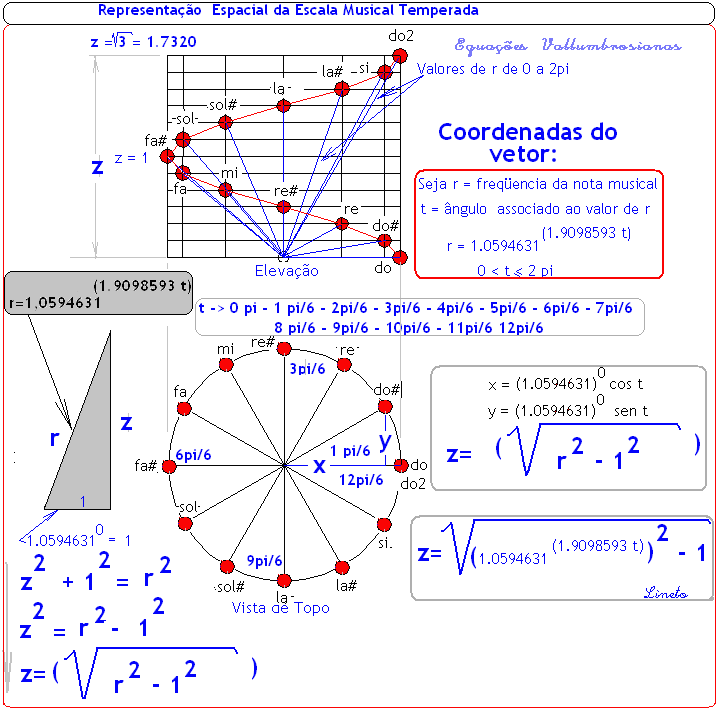
Aplicando as fórmulas acima podemos construir uma tabela das coordenadas do vetor posição no espaço tridimensional que representa cada nota musical da sequencia da escala musical igualmente temperada. O intervalo acima está limitado de 0 a 2pi, claro está que podemos estender este intervalos a quantas oitavas queiramos.

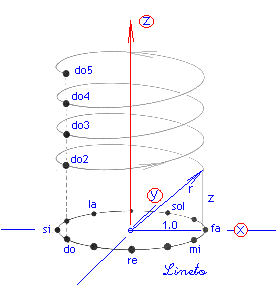
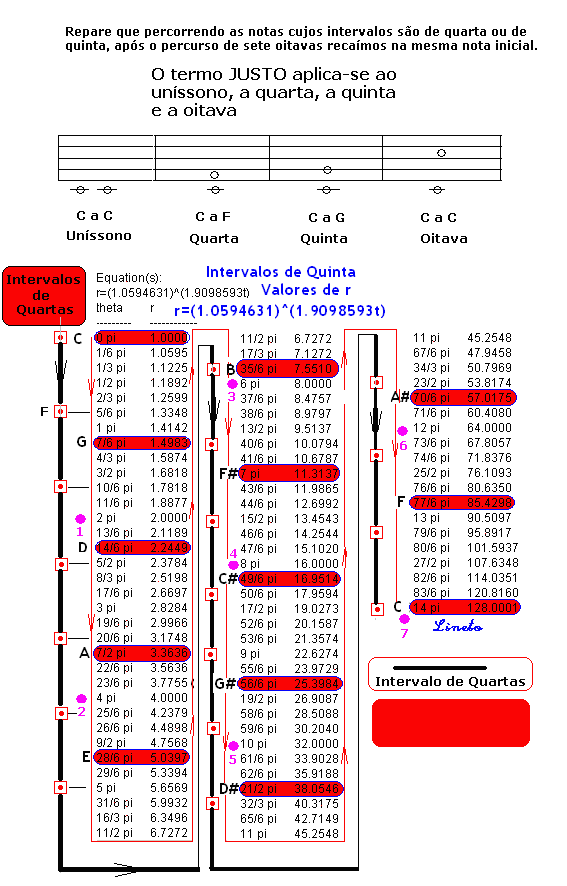
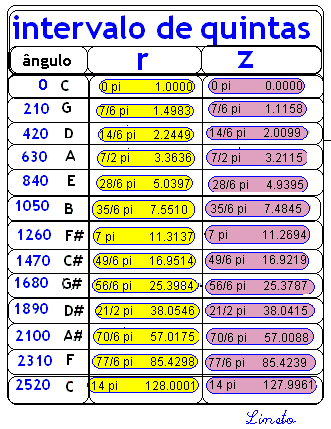
Representação Espacial da Escala Musical Temperada

Representação de uma oitava

Com esta visão espacial, os valores de r, nos intervalos de quintas – ficam de acôrdo com a tabela abaixo:

Incluímos também aqui os intervalos de Quarta.

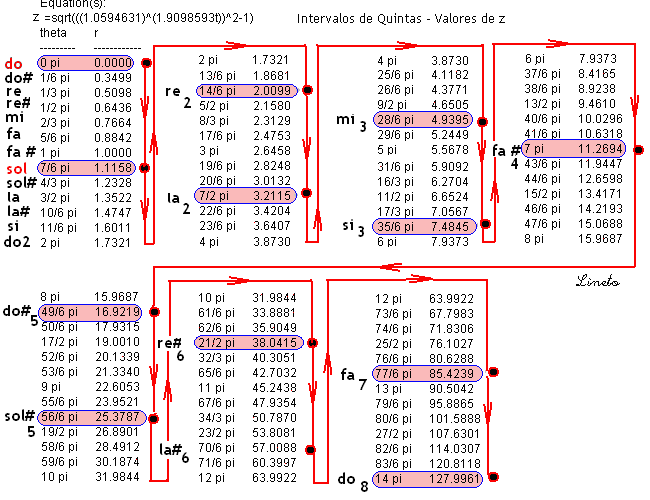
Com esta visão espacial, os valores de Z, nos intervalos de quintas – ficam de acôrdo com a tabela abaixo:

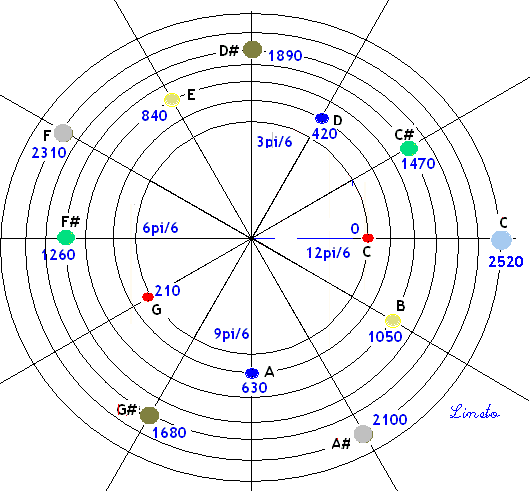
SEQUENCIA DOS INTERVALOS DE QUINTAS

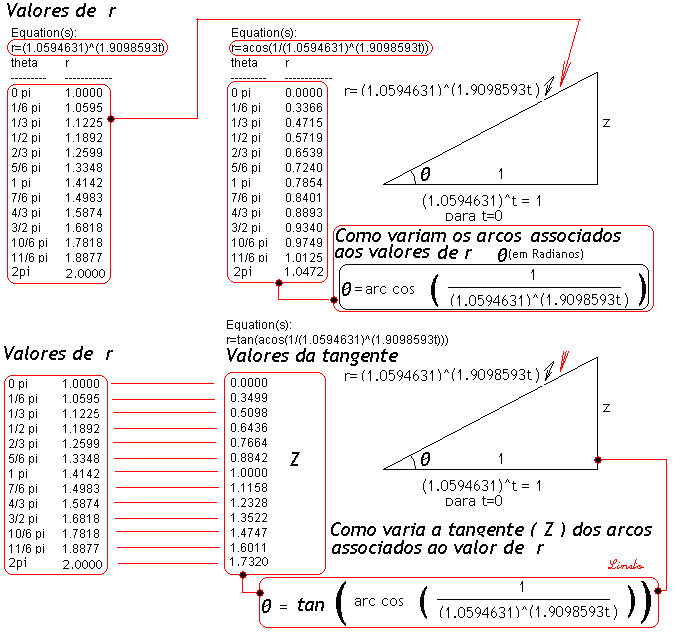
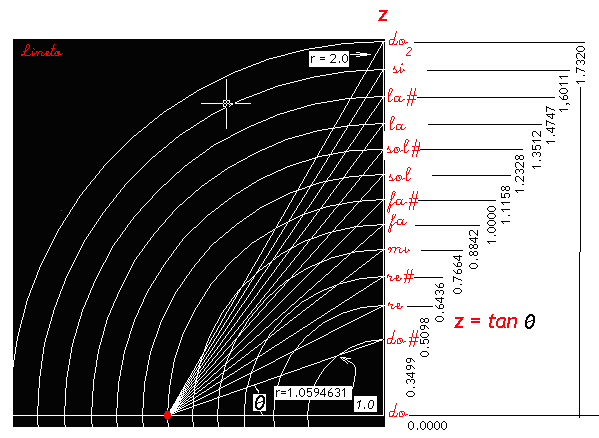
Os intervalos de quintas estão separados de 210 graus ou 7/6 pi radianos.

As notas estão representadas em círculos separados, mas na visão espacial tridimensional elas estão todas sobre a primeira circunferência, subindo em espiral de acordo o com a variação do raio r – (frequencia) da tabela acima.

ALGUNS CÁLCULOS COMPLEMENTARES

Como variam os ângulos associados a r (em radianos)

A cada valor de r da tabela à esquerda corresponde o seu ângulo de elevação

na tabela à direita – Primeira tabela abaixo -: Quando r=2, sua elevação é de 1.0471976 radianos ou 60 graus.