Coordenadas Polares

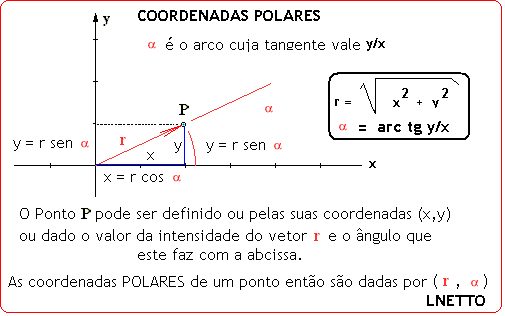
Assim se temos (r, alfa), imediatamente podemos transformar as coordenadas desse ponto dada em coordenadas polares para coordenadas cartesianas: Seja r = 5 e alfa = 25 graus, então:

y = r.sen(alfa)-> y = 5.sen 25 -> y = 5.0,4226182 -> y = 2,113091

x = r cos (alfa) -> 5.cos 25 -> x = 5.0,9063077 -> x = 4,5315385

ou fazendo o inverso, se temos as coordenadas x e y e queresmos as coordenadas polares:

Seja:

x = 4,5315385

y = 2,113091

e queremos expressar as coordenadas cartesianas desse ponto em coordenadas polares:

Qual é o ângulo?

O ângulo é dado pelo arco cuja tangente vale (2,113091/4,5315385)

A tangente que vale 0,4663076 é correspondente ao ângulo de 25 graus.

GRÁFICOS DAS FUNÇÕES

A FUNÇÃO SENO

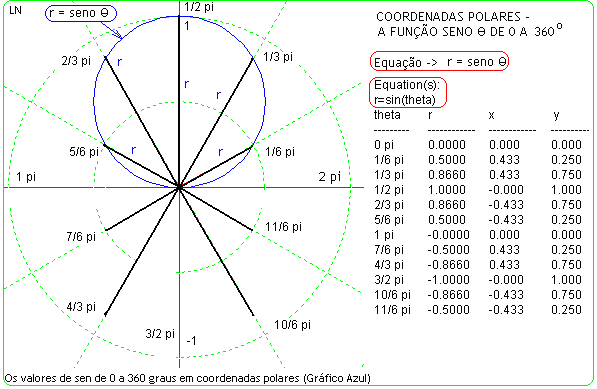
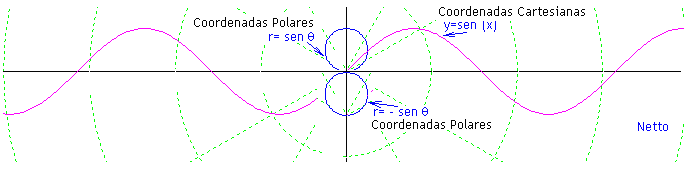
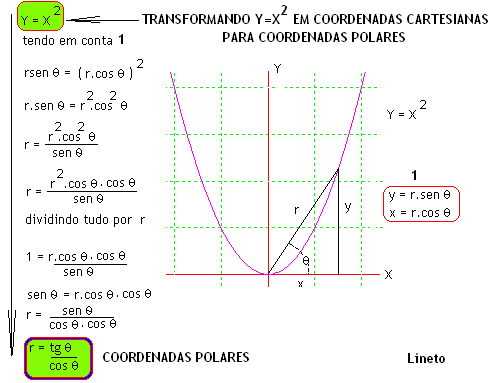
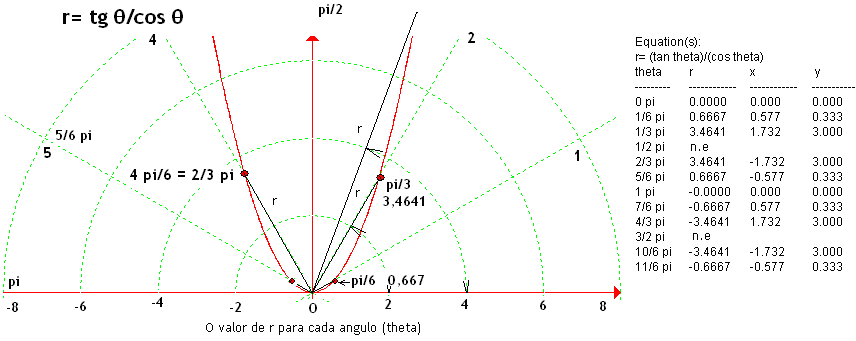
Compare a representação da função y = sen (x) em coordenadas polares e cartesianas.

Para cada valor de r (seno) há um ângulo associado.

Transformando y = x^2 em coordenadas cartesianas para coordenadas polares