Medidas dos Intervalos Musicais
por: Prof.Luiz Netto
Unidades de Medidas
O Cent – O Savart
O cent e o savart são unidades de medidas que permitem medir intervalos sonoros bem pequenos. A percepção da menor variação em frequência detectada pelo ouvido varia ao longo da faixa de áudio. O ouvido é bastante sensível aos sons graves e tem sua sensibilidade máxima entre 3,5 e 4.0 Khz, muito próximo da primeira zona de ressonância que ocorre no ouvido externo.
A segunda zona de ressonância ocorre próximo aos 13 Khz. A capacidade de distinção do ouvido em relação à menor variação de frequência, depende da frequência do som, da intensidade sonora, da duração do som, da velocidade de alteração, bem como do treino auditivo particular de cada individuo. Em sons graves mudanças de frequências de 1 hz podem ser detectadas.
Próximo a 1,0 Khz a maior parte das pessoas é capaz de distinguir mudanças de 3 Hz. Ao redor de 100 Hz mudanças na frequência podem ser notadas em 3 décimos de Hz. Portanto como vimos o limiar da percepção de variação é um valor variável ao longo da faixa de áudio.
|
O CENT
Normalmente lidamos com valores de ½ tom que na escala musical igualmente temperada é igual ao valor acima, ou seja 1,0594631. No entanto as vezes é necessário lidar com intervalos bem menores, daí surgiu a necessidade de se construir um sistema de medida com unidades menores. Assim foi criado o CENT que é este intervalo de ½ tom dividido em 100 partes. Assim de acordo com essa definição podemos construir uma equação que traduza isto, ou seja:
Aplicando logarítmos para resolver a equação, vem
Aplicando-se então a definição de logaritmos (O expoente de base 10 é que é o logarítimo de i) temos que:
Vemos então que o intervalo correspondente a um centésimo de ½ tom é igual a 1,0005777, este valor é portanto a razão da progressão geométrica cuja razão é este valor, o que vale dizer que teremos que multiplicar 1,0005777 por si mesmo 100 vezes, para alcançarmos 1/2 tom. Se pensarmos que no intervalo de uma oitava temos 12 intervalos então teremos 12*100 cents = 1200 cents e portanto se quisermos podemos repetir o mesmo raciocínio, podemos escrever:
Que é o mesmo resultado que chegamos quando calculamos a divisão em 100 partes. 0 SAVART Na unidade savart existe uma condição a ser satisfeita, qual seja que o log i seja igual a 1/1000. Lembando que logarítmo do número i é o expoente da potencia => log i = 0,001.
Esse intervalo, como pode se ver é bem maior que o intervalo do Cent que é igual a 1,0005777. Isto quer dizer que há muito mais cents em uma oitva do que savarts, lembrando que em um uma razão quanto mais diminui o denominador maior é o quociente entre dois números. Assim estabelecemos a equação
Porque estamos querendo saber qual o valor de x que satisfaz a equação e igualamos a 2 , porque sabemos que como cobrimos uma oitava, o valor da frequência do som deve dobrar nesse intervalo. Assim, x*log i = log2, isso implica que x = log2/log i. Como existe a imposição que log i = 0,001, temos que x = 0,30103/0,001, portanto x=301 Portanto podemos escrever que:
Agora que já sabemos que há 301 savarts em uma oitava, podemos calcular o menor intervalo dentro dessa escala de outra maneira:
O próximo passo é calcular intervalos utilizando as unidades de medidas cents e savarts |
O Prof.Luiz Netto é graduado em Matemática pela Faculdade de Filosofia de Ciências e Letras de Santo André – SP – Brasil








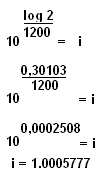
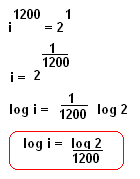
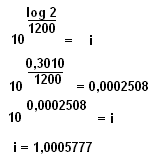

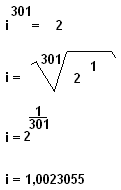 :
: