|
Teoria
Ondulatória
Tratamento
Matemático da onda
Parte 2
Prof.
Luiz Ferraz Netto
[email protected]
Essa
Parte 2 da Teoria Ondulatória contém:
Onda senoidal, Ondas
estacionárias e Vibrações próprias
A
onda senoidal (ou onda co-senoidal)
A onda mais importante e mais comum é a onda
senoidal (onda harmônica). Vamos considera-la, inicialmente no caso
unidimensional. A perturbação x
propagar-se-á com a velocidade u ao longo do eixo x. Na posição x
= 0 (onde se pode imaginar a localização da fonte
das perturbações) aparecerá uma perturbação periódica em relação ao
tempo: x(x
= 0,t) = A.sen wt
.
Como a perturbação
deve-se propagar com a velocidade inalterável u, obtém-se assim no
tempo t, para uma posição x, a mesma perturbação que
existira, há um certo intervalo de tempo t’ 'mais cedo', na posição
x = 0 tendo neste caso o “tempo de percurso” t' o valor
x/u . Portanto,
x(x,t)
= x(x
= 0,t - t') = A.sen w(t - t') =
A.sen (wt - wx/u)
.
Escreve-se,
comumente:
x(x,t)
= A.sen (wt - k.x)
A = amplitude
da onda,
j
= (wt - k.x) chama-se fase
da onda,
w
= pulsação ou freqüência circular (variação
da fase por segundo),
k = w/u
é o número da onda (variação da fase por
metro).
Da expressão
x = A.sen (wt
- k.x) vê-se que:
1) Para uma dada
posição (x = const.) x
varia periodicamente com o tempo (período T = 2p/w).
2) Para um dado
instante (t = const.), x
é espacialmente periódica. O período espacial chama-se comprimento da
onda l
(l
= 2p/k).
3) Pontos com
fase constante movem-se com a velocidade u. Observe: De j
= (wt - k.x) = const., obtemos,
por derivação: dj =
w.dt
- k.dx = 0, ou dx/dt = w/k
= u = vfase . Por isto dá-se
a u o nome de velocidade de fase.
4) O caráter da
onda não varia, ao se acrescentar à fase j
uma constante jo.
A adição de uma constante de fase significa
o mesmo que fazer a escolha de uma outra origem dos tempos (ou das posições).
Pondo-se por
exemplo, t = to + t’ torna-se assim: j
= (wt' - k.x) + jo.
Com uma escolha adequada da origem dos tempos, podem-se atribuir à
constante jo
valores quaisquer. Sendo jo
= p/2,
transforma-se a onda senoidal em onda co-senoidal:
sen (j
+ p/2)
= cos j
. Para jo=
p
, inverte-se o sinal: sen (j
+ p)
= - sen j =
sen (-j).
5) Da relação
x = A.sen (wt
- k.x) = A sen k(u.t - x) resulta que a onda senoidal é também uma
solução da equação das ondas.
Notemos ainda as
seguintes relações:

Observação:
Para muitos cálculos com ondas harmônicas e conveniente completar a
grandeza real x
= a cos j,
formando-se o número complexo a,
(cos
j
+ i.sen j)
= a.eij
.
No
fim dos cálculos voltamos novamente à parte real.
Ondas
estacionárias
As ondas estacionárias aparecem
muito freqüentemente nos meios limitados. Quando a onda chega aos limites
do meio, nos quais nenhuma transmissão de energia para o exterior é possível,
reflete-se e volta no sentido oposto.
Na ilustração
a seguir, a onda que se propaga para a direita pode ser expressa por: x1
= A.sen (wt - k.x) e a
onda refletida, que se propaga para a esquerda (inversão do sinal de u),
por: x2
= A.sen (wt + k.x) . As perturbações
x1
e x2
somam-se de acordo com o princípio da superposição:
x
= x1
+ x2
x(x,t)
= A.sen(wt
- kx) + A.sen(wt
+ kx) = 2A.coskx.senwt
O resultado
desta superposição é um tipo de onda completamente novo, a chamada onda
estacionária.
Vê-se que, para
um ponto determinado xo do espaço tem lugar uma vibração harmônica.
A amplitude porém varia de posição em posição, sendo para x = xo
: 2A.coskxo = 2A.cos(2p.xo/l).
Onde x for um múltiplo inteiro de l,
x será identicamente nula, isto
é, a amplitude é nula em todos os instantes (nós da vibração --- N,
na ilustração acima).
Há também posições,
nas quais a amplitude adquire seu valor máximo 2A. Estas posições
chamam-se ventres da vibração (V, na ilustração acima).
A formação de
ondas estacionárias por meio da reflexão de vibrações acústicas numa
parede pode ser evidenciada com o auxílio de uma chama sensível de gás
ou com um microfone (ilustração abaixo -- demonstração recomendada).
Numa posição correspondente a um nó o escoamento do gás é laminar
(chama longa); num ventre o escoamento é turbulento (chama curta).
Nos instrumentos
musicais criam-se ondas estacionárias. Por meio disto, fixam-se os números
de vibrações (alturas do som nos tubos e cordas sonoros).
Vibrações
próprias
As ondas estacionárias que aparecem nos meios confinados não
podem possuir freqüências arbitrárias, porém
somente determinadas freqüências próprias f1, f2,
f3 , ... Isto se vê
claramente no exemplo da corda vibrante.
Uma corda, presa em suas extremidades E, somente poderá
vibrar de modo que as extremidades constituam nós N. Chama-se a isto
condição de extremidade (ou fronteira).
À distância
entre dois nós vizinhos é igual à metade do comprimento de onda l.
Ao comprimento L da corda deve corresponder um número inteiro de
semi-comprimentos de onda l/2:
L = n.(l/2).
Sendo
entretanto, a velocidade de propagação u = f . l,
teremos:
f
= u/l
= u/(2L/n) = n(u/2L) = n.fo .
A vibração
correspondente a n = 1 chama-se vibração
fundamental; todas as demais são múltiplos inteiros de fo
e chamam-se vibrações superiores. Quando as
freqüências próprias estão entre si como 1:2:3:... (como neste caso)
diz-se tratar de vibrações superiores “harmônicas".
A cada estado de
vibração corresponde uma certa energia E. Em quase todos os
sistemas E diminui com o decorrer do tempo, porque, a energia se
transmite ao ambiente ou se transforma em outra espécie de energia
(calor). Por isto, praticamente, todas as vibrações são amortecidas. Sem
o amortecimento, todo sistema, uma vez adquirido um estado de vibração,
nele permaneceria: as vibrações próprias tem caráter estacionário.
Já que as
perturbações se superpõem simplesmente, segundo o princípio da
superposição, um sistema poderá vibrar simultaneamente com várias vibrações
próprias. Matematicamente, as vibrações
próprias são as soluções da equação das ondas que, em cada ponto do
meio, variam co-senoidalmente com o tempo e com um período T, independente
da posição.
x
= A(x,y,z).coswt
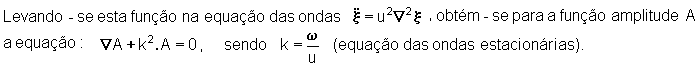
Além desta equação,
A deve satisfazer as condições de fronteira. (Por exemplo, no caso de uma
membrana presa segundo seu contorno, a
amplitude da vibração A, ao longo de seu perímetro deverá ser nula).
As condições
de fronteira fazem com que k e conseqüentemente f não assumam
valores quaisquer, porém somente os valores próprios k.
A cada valor próprio
kn corresponde uma freqüência própria e uma função própria
An.
Em lugar dos
pontos nodais, como no caso da corda, aparecem aqui linhas nodais. As linhas
nós podem tornar-se visíveis. Nas membranas metálicas isto
acontece cobrindo-as com areia. As
figuras criadas desta maneira chamam-se figuras de Chladny (ver demonstração
nessa sala).
Mais simples
ainda são as linhas nodais nas membranas quadráticas. Igualmente muito fáceis
de observar são as formas de vibração nas lâminas circulares. Nestas,
as linhas nodais são diâmetros e circunferências concêntricas, como se
vê no desenho devido a vibrações sonoras (ilustração abaixo). Para
cada desenho, obtido pelo som, corresponde um determinado número de vibrações
com o qual se produz a vibração considerada.
No caso de
membranas circulares as funções próprias são funções cilíndricas e
as vibrações fundamentais e superiores já não são “harmônicas".
|