Teoria Ondulatória
 Tratamento Matemático da onda
Parte 1

Prof. Luiz Ferraz Netto
[email protected]

Essa Parte 1 da Teoria Ondulatória contém: Fundamentos físicos; Velocidade de uma onda e Dedução da equação das ondas elásticas longitudinais.

Fundamentos físicos
A teoria ondulatória estuda a propagação de perturbações nos meios contínuos. O tipo do meio, bem como a espécie da perturbação, podem ser muito variados.
No caso das ondas superficiais o meio é um líquido; a perturbação consiste no deslocamento, x, das partículas de sua posição de equilíbrio.
Para as ondas sonoras o meio é um material sólido, líquido ou gasoso; a perturbação provém do aparecimento de um estado de superpressão local.
No caso das ondas eletromagnéticas (luz, ondas de rádio) não é necessário nenhum meio material. A perturbação consiste na criação de campos elétricos (magnéticos). (x, neste caso, é pois um vetor).

Como exemplo consideremos uma onda de compressão como a ilustrada abaixo:

Golpeando-se com um martelo a extremidade de uma barra metálica longa, cria-se assim, nesta extremidade da barra, uma perturbação (compressão). A princípio, a primeira camada tem sua pressão aumentada: suas partículas se afastam, por isto, da posição de equilíbrio a uma distância x, que serve como medida da perturbação. A perturbação se propaga, uma vez que as partículas individuais se vinculam reciprocamente, por meio de forças elásticas. As secções transversais vizinhas vão sofrendo sucessivamente um deslocamento e retornam ao equilíbrio: a perturbação “caminha”.

Para que a perturbação realmente se propague, e com isto se crie uma onda propriamente dita, a vinculação é essencial. Vê-se isto, de um modo particularmente claro, no caso da cadeia de ondas, um sistema de muitos pêndulos de torção ligados (experimento recomendado: clique aqui).

Na maioria dos casos, embora nem sempre, associa-se a uma propagação de ondas um transporte de energia.

Nas ondas devem-se distinguir as ondas transversais, em cujo caso a perturbação x é normal à direção da propagação (à esquerda, abaixo) e as ondas longitudinais, para as quais o deslocamento se dá na direção da propagação (à direita, abaixo)

Deve-se, contudo, observar que numa onda as partículas não se afastam continuamente, porém oscilam em torno da posição de equilíbrio. Essencial ainda, para toda a teoria ondulatória, é o princípio da superposição: duas perturbações da mesma espécie x₁ e x₂ compõem aditivamente uma perturbação resultante x = x1 + x2 .(Demonstração com ondas na água - cuba de ondas).

Velocidade de uma onda
A velocidade, com a qual uma perturbação se propaga, somente se poderá definir de uma maneira simples quando a perturbação não varia sua forma espacial. Limitar-nos-emos inicialmente a este caso, restringindo-nos aqui a lidar com um problema unidimensional (Exemplo: ondas sinuosas numa corda tensa -- ver experimento).

Caracterizamos a perturbação por meio de uma grandeza x, que é função da posição e do tempo.

Para que uma tal função constitua uma onda, deve satisfazer à condição seguinte: A perturbação x deve ter, para os diversos pontos da reta x, para o tempo t = 0, os valores dados na curva A:  x(x,0) = f(x) .

Esta onda deve se mover com a velocidade de propagação u dirigida para a direita (segundo os valores crescentes de x). A perturbação que, para o tempo t (curva B), achamos numa determinada posição x, apresentara-se, para t = 0, na posição  x_o = x - ut .
Será, portanto:

x(x,t) = x(x_o,0) = f(x_o) = f(x - ut)

Vemos portanto, que uma função que contém x e t somente na ligação (x - ut), constitui uma onda que se propaga com a velocidade u. A velocidade de propagação u depende das propriedades do meio transmissor. Com a ajuda de considerações dimensionais, pode-se muitas vezes determinar u, a menos de um fator numérico.

Exemplo - 1: No caso de ondas longitudinais elásticas, u deve depender do módulo de elasticidade E (módulo de Young) e da densidade absoluta r:   u = f(r,E).
Sendo porém,

Para o aço (E = 2,2 x 10¹¹ newton/m² ; r =  7 800 kg/m³)  torna-se u = 5 000 m/s.

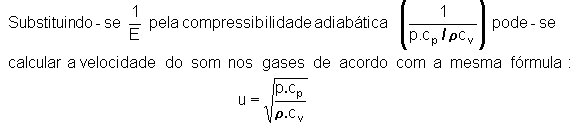
Exemplo - 2: Na propagação de ondas aquáticas em águas rasas (ondas pesadas), entra em jogo a profundidade h da água bem como a grandeza da aceleração da gravidade g e, portanto:  u =f(h,g) .

A massa não figura neste caso, como em todos os movimentos, devido ao peso (massa inerte = massa pesada). Como

[u] = m.s^-1  ,   [h] = m     e    [g] = m.s^-2

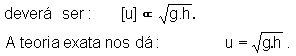
Para h = 0,05 m,   g = 9,81 ms^-2  será   u = 0,7 ms^-1.

Dedução da equação das ondas no exemplo de ondas elásticas longitudinais.
Consideremos uma barra bem longa, tendo secção transversal de área A, densidade r e módulo de elasticidade E. Uma onda corre no sentido dos x crescentes (ilustração abaixo).

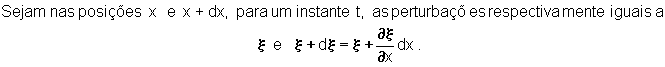
Neste caso a perturbação consiste no deslocamento das partículas de uma secção transversal a uma distância x, na direção x. Estes deslocamentos processam-se sob a influência de tensões elásticas t (tração, compressão; t = F/A). Designaremos a tração na posição x, no instante t, com t (x, t); na posição x + dx a compressão será, então, igual a

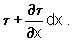
Visualizemos, agora, o elemento da barra compreendido entre as duas secções x e x + dx.  Os deslocamentos

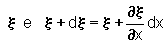
nas suas extremidades são diferentes. Este elemento da barra alongou-se, portanto, sob a influência das forças.

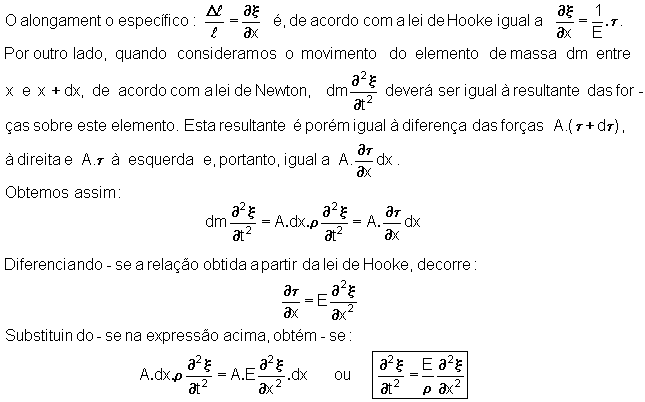
Esta é a chamada equação das ondas para a onda elástica ao longo de uma barra.

Veremos, a seguir, que a expressão representativa de uma onda longitudinal propagando-se ao longo do eixo  x , a saber,  x = f(x - ut) , satisfaz realmente à equação de ondas.

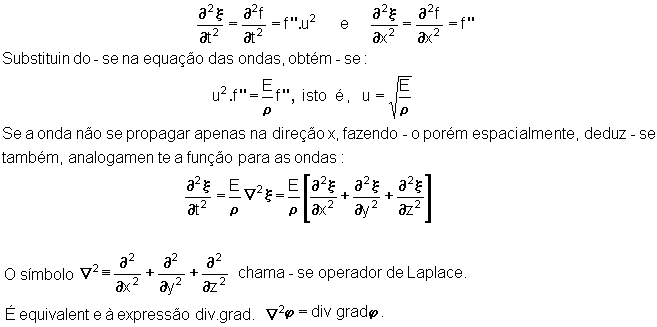
Segue Tratamento matemático da onda - Parte 2.