Questões de Ondulatória
Série C

Prof. Luiz Ferraz Netto
[email protected]

Questão 1
Prove que toda função da forma simples y = f(x ± ut), onde u é uma constante, satisfaz à equação unidimensional de onda.

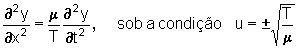
Solução
Partindo da função dada, vamos calcular as primeiras e segundas derivadas dessa função, a saber:

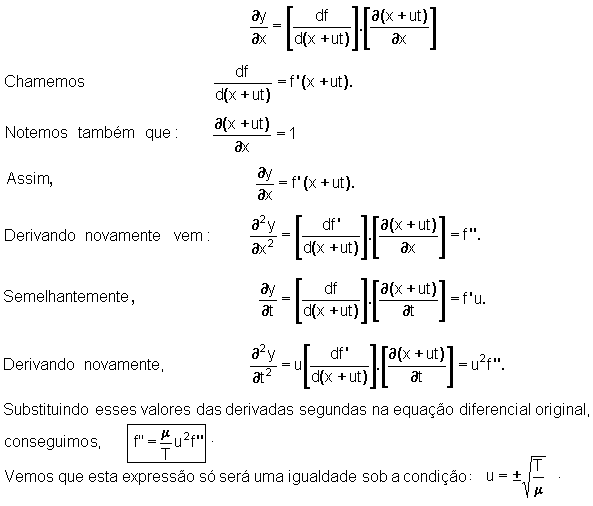
onde u é a velocidade de propagação, em grandeza. O sinal (+) indica o sentido de propagação da onda da esquerda para a direita e o sinal (-), o sentido contrário.

Consideremos alguns exemplos de funções da forma  y = f(x + ut):

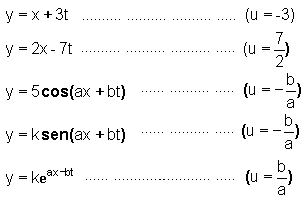
Questão 2
Sendo y = f(ax + bt) a forma completa da função dependente do tempo, que satisfaz à equação unidimensional de onda, ache a velocidade de propagação, u, de um dado ponto do pulso.

Solução
Para um dado ponto do pulso, o deslocamento é constante, isto é,  y = constante = f(ax + bt), então:

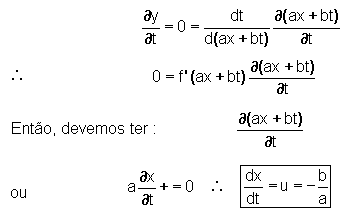
Questão 3
Calcule a energia total, E, no movimento ondulatório.

Solução
Seja a função de onda  y = A.sen(kx - wt),  onde k é o número de onda e w a pulsação. A energia cinética, E_cin., de um elemento de massa  dm  da corda (ou meio elástico), é:

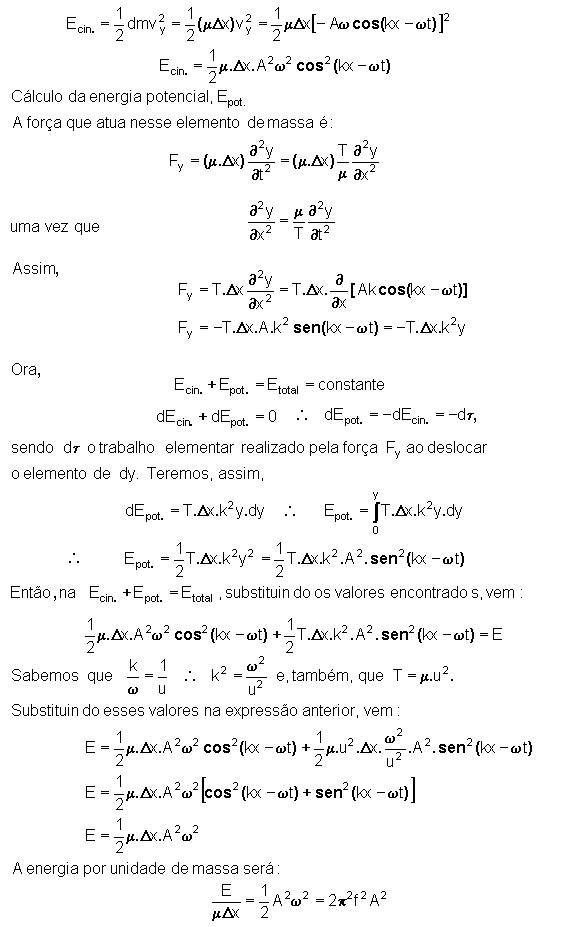
Questão 4
Uma perturbação periódica propaga-se ao longo de uma corda infinita que jaz ao longo do eixo dos x de um sistema de coordenadas cartesianas. A perturbação pode ser representada analIticamente pela equação   y = 7 sen (5x + 3t),   onde x é expresso em centímetros e t em segundos.
Pergunta-se:
(a) qual o deslocamento transversal máximo?;
(b) qual é o comprimento de onda?;
(c) está a perturbação movendo-se no sentido + x ou - x?;
(d) qual é a freqüência?;
(e) qual é a velocidade transversal máxima e a velocidade de propagação?;
(f) qual seria a equação mais geral, capaz de representar a perturbação e satisfazendo a equação de onda?

Solução
(a) O deslocamento transversal máximo implica no valor máximo para o seno, isto é, sen(5x + 3t) = 1. Então, Y_máx. = 7 cm (A = 7 cm, é a amplitude da onda senoidal).

(b) Comparando a função dada com a forma geral da função de onda   y = A sen (kx + wt),   temos:

k = 5 cm^-1 , portanto, 2p/l = 5 cm^-1 , portanto  l = 2p/5  cm.

(c) A onda se propaga para a esquerda, uma vez que, para um valor constante da fase  5x + 3t = const., o valor de x diminui com o crescer da variável t.

(d) Sendo  w = 3 s^-1 = 2pf, vem:  f = 3/(2p) Hz.

(e) Em valor absoluto, a velocidade de propagação será: u = l.f = (2p/5)(3/2p) = 0,6 cm/s. Algebricamente, será:  u = -(b/a) = -(w/k) = - 06 cm/s.

Vamos ao cálculo da velocidade transversal,  v_y = dy/dt = 21.cos(5x +3t). Nota:usei d  como derivada parcial.
O valor máximo implica no valor máximo do coseno, e teremos,  v_y = 21 cm/s.

(f) A função mais geral seria:  y = 7.sen(5x + 3t) + 7.sen(5x - 3t),  isto é, uma combinação de funções que satisfazem à equação de onda.

Questão 5
Dada a função de onda  y = 2.sen2p(0,1.x - 5.t),  onde  x  está em metros e  t  em segundos, calcular:

(a) o deslocamento transversal máximo;
(b) o comprimento de onda;
(c) a freqüência da perturbação;
(d) a velocidade transversal máxima;
(e) a velocidade de propagação do pulso;
(f) o período.

Solução
(a) O deslocamento transversal máximo, y_máx., implica no valor máximo para o seno, isto é,
sen2p(0,1.x - 5.t) = 1. Então,  y_máx. = 2 m (essa é a amplitude A da onda).

(b) Comparando a função dada com a forma geral da função de onda [ y = A.sen2p(x/l - t/T) ], temos:
      1/l = 0,1 m^-1 , portanto, l = 10 m.

(c) Vemos que 1/T = f = 5 s^-1 = 5 Hz.

(d) Calculemos primeiro a velocidade transversal, por derivação:  v_y = dy/dt = 2(-10p)cos(px/5 - 10pt).
      O valor máximo da velocidade implica no valor máximo do coseno, e teremos:  v_y = -20p m/s.

(e) A velocidade de propagação do pulso será:  u = l.f = 10 m.5 s^-1 = 50 m/s .  O pulso move-se no sentido +x.

(f) O período T = 1/f = 1/5 s.