Questões de Ondulatória
Série B

Prof. Luiz Ferraz Netto
[email protected]

Questão 1
Um fio de aço de 6 m de comprimento tem uma massa de 60 g e é esticado com uma tensão de 1000 N. Qual é a velocidade de propagação de uma onda transversal no fio?

Solução
Sabemos que uma propriedade característica de uma onda unidimensional é que a velocidade de propagação é independente da amplitude da perturbação e só depende das propriedades características do meio (fio), isto é, da tensão e da massa específica linear. Teremos, assim, a grandeza da velocidade de propagação:

Questão 2
A corda de uma guitarra tem 30 cm de comprimento e uma massa de 100 g. Que tensão deve ter essa corda para que dê uma freqüência de 262 Hz, correspondente à oscilação fundamental?

Solução
A tensão da corda é dada pela expressão T = m.u²  onde  m = m/L = 100 g/ 30 cm = 3,33 g/cm.

Podemos achar u (velocidade da onda transversal) pela relação u = l.f . Como a oscilação é fundamental, temos dois nós, um em cada extremidade, e  l/2 = L , portanto,  l = 2L = 60 cm.

Assim,  u = l.f = 60 cm x 262 Hz = 1,572.10⁴ cm/s. Substituindo esse valor na expressão de T, vem:

T = 3,33.(1,572 X 10⁴)² = 8,25 x 10⁸ dinas.

Esta força é muito grande para ser suportada por uma mola leve. Por esta razão, as cordas dos instrumentos musicais são usualmente feitas de ligas metálicas fortes.

Questão 3
Prende-se a extremidade de um tubo de borracha num suporte fixo. A outra passa numa roldana, a 8 m da primeira e suporta massa de 2 kg. A massa do tubo, entre a extremidade fixa e a roldana, vale 600 g. Qual a velocidade de uma onda transversal de pequena amplitude, no tubo? Adotar g = 9,8 m/s².

Solução
A tração no tubo de borracha é dada pelo peso da carga suspensa T = P = m.g = 2 X 9,8 = 19,6 N.
A massa específica linear do tubo é m = m/L = 0,6 kg/ 8 m = 0,075 kg/m. A velocidade de propagação será:

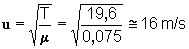
Questão 4
Uma onda senoidal, de amplitude A = 10 cm e comprimento l = 3 m, desloca-se no referido tubo (questão 3), da esquerda para a direita. Qual a velocidade transversal máxima de um ponto do mesmo?

Solução
Como a onda desloca-se da esquerda para a direita, a função da onda será y = A.sen(kx - w.t), onde k representa o número de onda ou constante de propagação e w a pulsação.
Sua velocidade transversal será:

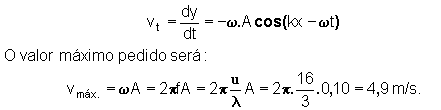
Questão 5
A que tensão deve estar submetido um fio de bronze, cuja área da seção transversal é 10^-2 cm², para que as velocidades das ondas longitudinais e transversais, ao longo do mesmo, sejam iguais? O módulo de Young do bronze é 9,1 X 10¹¹ dinas/cm². É esta situação física realizável?

Solução
A velocidade das ondas transversas no fio é dada pela expressão:

onde Y é o módulo de Young de alongamento do fio e r a massa por unidade de volume.

De acordo, com o enunciado, deve-se ter  u_T = u_L ; logo:

sendo m = m/L e r = m/V = m/A.L, temos  m/r = A, que é a área da seção transversal do fio.

Teremos, então,  T = A.Y  e, numericamente, T = 10^-2 cm² x 9,1 X 10¹¹ dinas/cm² = 9,1 x 10⁹ dinas.

Desde que a fórmula do módulo de Young é   Y = (T/A)/(DL/L), a expressão T = A.Y implica DL/L = 1.
O limite elástico do fio teria sido ultrapassado muito antes deste ponto. A situação é, assim, fisicamente irrealizável, e ondas longitudinais sempre viajarão mais rápidas do que ondas transversais, no mesmo fio.