Questões de Ondulatória
Série A

Prof. Luiz Ferraz Netto
[email protected]

Questão 1
Como se movimentam os pontos de um meio no qual se propaga um pulso?

Solução
Consideremos um pulso “para cima”, movendo-se ao longo de uma mola ou corda tensa, da esquerda para a direita, de acordo com a ilustração, onde o pulso foi estilizado.

Seja u a velocidade de propagação do pulso. Vemos, pela figura acima, que os pontos do meio movem-se paia cima e para baixo. Isto é verdadeiro, quer o pulso se mova da esquerda para a direita ou vice-versa.
Desse modo, os pontos do meio movimentam-se independentemente do sentido da velocidade de propagação. Para sabermos qual é o sentido da propagação devemos nos utilizar da informação inicial "pulso para cima"; assim ficamos sabendo qual é a "frente do pulso". Os pontos da "frente do pulso" devem iniciar seus deslocamentos "para cima". Na ilustração acima a indicação do sentido da velocidade (==>) poderia ser dispensado, pois ainda assim saberíamos que o movimento se dá da esquerda para a direita.

Questão 2
Faça a seqüência dos gráficos que mostram os deslocamentos e as velocidades dos pontos de um meio unidimensional, quando dois pulsos se cruzam, um através do outro.

Solução
Suponhamos dois pulsos, para cima, deslocando-se um contra o outro, com a mesma velocidade de propagação u = 1 divisão/segundo.

Na ilustração acima os pulsos foram “estilizados” para facilitar a compreensão. Observe que no deslocamento máximo os pontos do meio estão em repouso.

Questão 3
Quais são os fatores que determinam a velocidade de um pulso de partida?
A velocidade será a mesma para uma fila de caminhões e uma fila de automóveis?

Solução
Um “pulso de partida” desloca-se em sentido contrário ao movimento dos carros, com uma velocidade tanto maior quanto menor for o intervalo de tempo entre as saídas dos carros na fila. Há fatores subjetivos, técnicos e externos que podem influir nesse intervalo de tempo, muito mais do que a aceleração do veículo. Podemos citar: a) atenção ao sinal; b) tempo de reação do motorista; c) hábitos de segurança no guiar; d) condições do veículo e do terreno etc.

Desde que os tempos de reação entre os motoristas dos carros e caminhões sejam os mesmos, os carros aceleram mais rapidamente do que os caminhões, pois possuem menor inércia. O pulso de partida entre os caminhões será mais vagaroso. A questão completa exige saber: o que o motorista emprega como “sinal de partida”?

Questão 4
Suponha que você tem um meio formado por três seções de corda: leve, pesada e leve. Se você a sacode por um extremo, formando um pulso, que acontecerá?

Solução:
Esta questão merece uma experimentação real; deve ser produzida, na prática, utilizando-se cordas ou molas helicoidais, de massas específicas diferentes, a fim de fixar a compreensão do aluno.
Seja o esboço dado na ilustração:

Em cada junção, A ou B, o pulso será parcialmente transmitido (refração) e parcialmente refletido (reflexão). Quanto maior a diferença entre as massas especificas das cordas, tanto maior será a fração refletida.

Observe que a velocidade do pulso será menor na corda mais pesada. Disso se conclui que d₁ é maior do que d₂ e l₁ é maior do que l₂. Assim é que temos:

Questão 5
Numa cuba de ondas, quando se produz um pulso cada 1/10 s, verificamos ser l igual a 3 cm.
a) Qual é a velocidade de propagação do pulso na água?
b) No mesmo meio, produzimos dois pulsos, o segundo, 0,5 s após o primeiro. Qual é a distância que os separa?

Solução
a) Se o período é T = 1/10 s, a freqüência será f = 1/T = 10 pulsos/s.
Desse modo, a velocidade de propagação da onda será:

v = lf = 3cm.10pulsos/s = 30 cm/s.

b) O primeiro pulso percorreu, nesse intervalo de tempo de 0,5 s, uma distância de  d = v.t = 30(cm/s).0,5(s) = 15 cm. Portanto, o primeiro está adiantado 15 cm em relação ao seguido.

Questão 6
Uma onda, formada em uma cuba de ondas, passa de urna seção rasa para outra profunda, sob um ângulo de incidência de 45^o e um ângulo de refração de 60^o.
a) Qual é a razão das velocidades nas duas seções?
b) Se a velocidade da onda é de 25 cm/s na região profunda, quanto vale na seção rasa?

Solução: a) Consideremos o pulso de onda, AB, aproximando-se do cais (interface entre as regiões rasa e funda), em três posições sucessivas, de acordo com a ilustração:

Consideremos os dois deslocamentos DD’ e CC’ que se processam no mesmo intervalo de tempo (Dt), sendo v₂ e v₁ as velocidades de propagação, respectivas, nas regiões rasa e funda. Teremos:

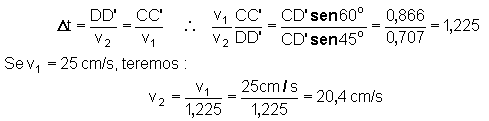
Questão 7
a) Um pneumático de automóvel tem uma circunferência de 2,10 m. Se a roda gira 200 vezes por minuto, qual é a velocidade do automóvel em metros por minuto?

b) Uma onda luminosa cuja freqüência é de 6,0 x 10¹⁴ Hz passa através de um líquido. Mede-se o comprimento da onda dentro do líquido e obtém-se, para seu valor, 3,0 X 10^-5 cm. Qual é a velocidade da luz neste líquido?

c) Qual é o comprimento da onda no vácuo a partir do qual foi calculada a freqüência?

d) Qual o índice de refração do líquido?

Solução
a) Em cada giro da roda, sem deslizar, o carro percorre 2,10 m; logo, nos 200 giros da roda o carro percorrerá:

D = 2,10 m/giro X 200 giros/min = 420 m/min.

b) Nesse item (b) da questão, estaremos admitindo duas hipóteses: 1) a luz é onda; 2) a freqüência da luz não muda quando ela passa de um meio para outro.

Ora, com  l = 3,0.10^-5 cm  e  f = 6,0.10¹⁴ Hz,  teremos:  v = lf = 3,0.10^-5 . 6,0.10¹⁴ = 1,8.10¹⁰ cm/s.

c) Sendo a velocidade da luz no vácuo c = 3,0.10¹⁰ cm/s, para o comprimento dessa onda, no vácuo, teremos:

l_vácuo = v/f = (3,0.10¹⁰)/(6,0.10¹⁴) = 5,0.10^-5 cm.

d) O índice de refração do líquido vem dado por:

n = c/v_líq. = (3,0.10¹⁰)/(1,8.10¹⁰) = 1,7.

Questão 8
Aumentando-se a tensão de uma corda o que acontece com o número de nós?

Solução
De acordo com a expressão da velocidade de propagação da onda na corda tensa,

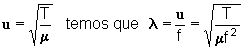
Aumentando-se T, aumenta-se l, o que implica no aumento da distância entre dois nós consecutivos e na diminuição do número deles.