Período de oscilação

Prof. Luiz Ferraz Netto
[email protected]

Introdução
Considere a seguinte situação: uma partícula de massa m se desloca com velocidade V entre duas paredes de grande massa, com as quais  ela experimenta colisões perfeitamente elásticas. O movimento resultante, caso a velocidade mantenha-se sempre perpendicular às paredes, será algo como um 'pingue-pongue' perpétuo. Abaixo ilustramos a situação proposta e o gráfico s = s(t), de origem centrada a igual distância das paredes. Nesse sistema, a coordenada s coincide com a coordenada x.

Obviamente, esse é o gráfico de um movimento periódico. O período do movimento não se altera com o decorrer do tempo. Entretanto, não podemos dizer que ele seja o período próprio do sistema, pois com diferentes condições iniciais obteremos um período diferente.
Basta, por exemplo, que aumentemos o módulo de V para obter um novo movimento periódico cujo gráfico poderá ser algo assim:

Podemos notar ainda que, se diminuirmos a distância entre as paredes, mantendo a velocidade primitiva, o período diminuirá, e o gráfico será algo como:

Portanto, o período do movimento não depende apenas do sistema, mas também das condições iniciais. No exemplo acima, alterar a velocidade inicial da bola, a distância entre as paredes ou ambos, afetará o período do movimento.

O mesmo ocorrerá com esse outro sistema: um pequeno bloco desliza, sem atrito, sobre um duplo plano inclinado em forma de 'V' (negligenciamos a descontinuidade na interseção). O bloco é abandonado de uma particular altura h, sendo uniformemente acelerado até o centro do "vale do potencial" e, em seguida, desacelerado uniformemente até atingir a mesma altura inicial no outro plano inclinado. Eis a situação e o correspondente gráfico do movimento:

Cuidado! A figura tem certas semelhanças qualitativas com uma senóide, mas é formada com ramos de parábolas!
O período certamente depende das condições iniciais: se soltarmos o bloco de uma altura menor (h' < h), haverá menor distância a percorrer, o que se efetuará em menor tempo (lembre-se que a aceleração tem módulo constante a = g.senq). O novo gráfico será algo como:

Novamente temos em mãos um sistema que produz um movimento periódico, mas cujo período depende das condições iniciais, e não apenas do sistema considerado.
Pergunta: Será que existem sistemas cujo período de movimento sejam independentes das condições iniciais?
Resposta: Sim. E isso nos trará conceitos importantes, que culminará com o fenômeno da ressonância.

Imagine a seguinte situação:

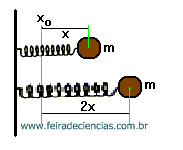
Duas massas iguais estão ligadas à duas molas ideais, de mesma constante elástica e mesmo comprimento natural. Não existe atrito contra o plano horizontal que suporta a massa m (não representado na ilustração). Suponha que distendamos a segunda mola do dobro da primeira. Em seguida, soltamos as duas massas simultaneamente, de modo que elas "apostam corrida" até a posição de equilíbrio xo . Qual das massas chegará primeiro?

Aparentemente, existem dois fatores que atuam em sentidos opostos: a força de restituição e a distância a ser percorrida. Na segunda situação, a distância a ser percorrida até a posição de equilíbrio é maior (2x), mas a força que atua na massa também é maior (maior deformação da mola).
Qual dos fatores será predominante?

A resposta experimental é: nenhum deles. As duas massas chegam exatamente ao mesmo tempo.
O argumento matemático que ajuda a compreender o motivo dessa coincidência é ilustrado abaixo:

A um pequeno deslocamento inicial Dx da massa com mola menos distendida corresponde um deslocamento duplo 2.Dx da outra massa. Fácil ver que a força na segunda situação, em cada posição até a posição de equilíbrio, é o dobro daquela da primeira situação. Ao passarem pela posição de equilíbrio a massa da segunda situação terá o dobro da velocidade da primeira.

Para bem visualizar isso, poderemos usar de uma barra muito leve interligando os dois sistemas e capaz de girar, sem atrito, sobre um eixo colocado à altura da posição de equilíbrio. A barra acompanhará a cada instante os movimentos das duas massas. Veja isso:

Em resumo, o tempo que qualquer das massas leva para voltar à posição de equilíbrio (x_o) é o mesmo, independente das condições iniciais. Pela conservação da energia, e por um argumento de simetria, pode-se mostrar que, após cruzar a 'linha de chegada' (x_o), as duas massas passarão a ser 'freadas' pela mola, parando após um tempo igual ao necessário para acelerá-las a uma distância igual à que seus pontos de partida tinham ao ponto de equilíbrio, ou seja, uma das massas avançará x acima da posição x_o e a outra 2x.
Ilustramos isso abaixo, com deslocamentos iniciais d e D = 2d, com molas no plano horizontal, sem atrito:

O resultado é um movimento periódico cujo período independe das condições iniciais, e que é o período próprio do sistema massa-mola. Como sabemos, esse período é expresso por:

Comprovação experimental
Munido de uma mola de constante elástica K conhecida e da massa m, também conhecida, meça o período de oscilação própria do sistema massa-mola. Caso o período seja muito pequeno para ser medido diretamente com um cronômetro, meça o tempo necessário para que o sistema complete, por exemplo, dez ciclos completos, o que aumentará sua precisão.
Faça o sistema oscilar com grande amplitude e meça o período. Em seguida, repita a medida para oscilações bem pequenas, comparando-os.

Procure estabelecer a relação entre suas observações tiradas do sistema massa-mola e o fato de que um objeto de metal dá sempre o mesmo som quando percutido com forças diferentes (o que varia é a intensidade do som, propriedade popularmente denominado por 'volume do som'). Já imaginou se um sino desse um som diferente para cada percutida com intensidade diferente? E o xilofone? E o piano?

Muita atenção a isso!
Talvez, durante algumas experiências, você tenha estranhado o fato da mola estar na vertical. A ação da gravidade não deveria alterar a lei de força em função da posição? Afinal, há uma nova força atuando.
Uma análise gráfica mostra que há realmente uma diferença, mas verificamos que ela não altera essencialmente as características do movimento. O período do sistema massa-mola não se altera, uma vez que  na 'nova lei de força' a resultante das duas forças continua a ser de 'restituição do tipo elástica'.
Observe:

Assim, um sistema massa-mola NÃO TEM seu período alterado pela ação da gravidade.

Para fazer experiências com isso basta você dispor de uma mola e um carrinho dotado de rodas. Teste o experimento na horizontal e na vertical. Compare seus períodos. Use o método de contagem cumulativa dos ciclos completos, para melhorar a precisão.
Coloque uma carga extra no carrinho e experimente novamente, tanto na horizontal como na vertical. compare os períodos. Mantenha o carrinho, mas troque a mola. Repita tudo.
Constate que cada sistema massa-mola tem seu período próprio de oscilação. Do que depende esse período? quais os parâmetros relevantes?

Para demonstrações aos alunos, recomendamos ao professor, adquirir uma coleção de molas de constantes elásticas diferentes e massas aferidas, montadas conforme se ilustra:

Lembre-se de destacar aos alunos a seguinte observação 'intuitiva': 'as coisas grandes e pesadas são lentas'. [Não leve essa observação ao extremo, tá bem?].