Matemática na Música – Capítulo 4

Equação da Vibração de uma Corda Musical

4.2.1. Vibração pontual da corda

Consideremos uma partícula de massa m que possui uma posição de equilíbrio y = 0. Se essa partícula for sujeita a uma força F que atue sobre ela em direção à sua posição de equilíbrio, de forma a que , ou seja, a sua magnitude seja proporcional à distância y da sua posição de equilíbrio, então essa partícula descreve um movimento harmônico simples. Este tipo de movimento é descrito por qualquer partícula de uma corda que esteja a vibrar. Assim, seja y a ordenada de uma partícula de uma corda de um instrumento musical, que se move em torno da sua posição de repouso – o eixo dos xx. Na equação acima, k é apenas uma constante de proporcionalidade.

Considerando a Lei de Newton F = ma, em que a = , resulta que .

As soluções desta equação são da forma , em que as constantes A e B são determinadas pela velocidade e posição inicial da corda.

Os guitarristas utilizam freqüentemente uma técnica que consiste em colocar a corda a vibrar com um dedo colocado sobre ela, sem fazer pressão. Para obtermos sons através deste processo, temos que colocar o dedo sobre a corda em pontos estratégicos: a razão entre o comprimento da posição onde se encontra o dedo até um dos extremos, com o comprimento total da corda, deverá ser um número racional! Habitualmente, os guitarristas obtêm este tipo de sons colocando o dedo a meio, dois terços ou a três quartos da corda, originando assim sons mais “puros”, aos quais chamam harmônicos [1].

Se a equação de uma partícula da corda a vibrar livremente, for , então será a equação dessa mesma partícula quando se faz a corda vibrar com um dedo no centro (a partícula não poderá estar no centro da corda, pois assim permanecerá imóvel) e será a equação do ponto, quando esta vibra com um dedo colocado à distância de 2/3 do comprimento da corda a um dos extremos (e como anteriormente, a partícula não poderá estar a essa mesma distância de um dos extremos, pois assim permanecerá imóvel).

Os outros modos de fazer vibrar a corda dão origem a vibrações com pouca intensidade, pelo que os sons são quase imperceptíveis.

Se colocarmos uma corda a vibrar livremente e de seguida colocarmos um dedo a meio sem fazer pressão, constata-se que, ao contrário do que seria de esperar, a corda continua a vibrar. Tal deve-se ao fato de, na vibração livre de uma corda, estarem incluídas também as vibrações relativas aos harmônicos, pois são estes que originam o som, uma vez que o movimento associado à vibração inteira da corda foi impedido. A equação do movimento de uma partícula da corda é uma combinação de todas as formas possíveis de se fazer vibrar uma corda:

.

A legitimidade de se poder escrever assim o movimento de uma partícula será mais clarificado à frente.

Os coeficientes A_n e B_n representam as diferentes intensidades do harmônico n (que está associado à vibração que “divide” a corda em n partes iguais), presente no som que a corda produz. A variação relativa destas amplitudes depende das diversas formas possíveis da corda vibrar: livremente ou impedindo-a de vibrar em alguns pontos, atacando-a com um martelo, como no piano, com um arco de violino, com uma palheta, com os dedos …

Abordaremos de seguida o problema de uma forma mais geral, tentando compreender a vibração de uma corda na sua globalidade, ao mesmo tempo que constataremos a possibilidade de escrever a equação de uma corda como série de senos e cossenos, pois é uma conseqüência da abordagem global do problema.

4.2.2. Vibração geral da corda

Consideremos o segmento num gráfico cartesiano de duas dimensões, representando uma corda, de extremos 0 e l, no estado de equilíbrio. Para cada instante t, vamos considerar que a “partícula” da corda de abcissa x, tem ordenada . Iremos aqui tentar descobrir o máximo de informações acerca , pressupondo que os valores assumidos por são sempre de uma ordem de grandeza inferior à de l (estamos a assumir que a variação dos deslocamentos verticais da corda são pequenos).

Se focarmos as nossas atenções numa pequena porção da corda delimitada pelas abscissas e , podemos elaborar o seguinte esboço:

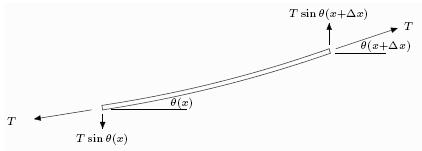
T – tensão a que a corda está submetida (em newtons = kg m/s² )       – amplitude do ângulo da corda com o eixo horizontal

O ângulo é a componente vertical da força exercida no extremo direito do segmento e é a componente vertical da força exercida no extremo esquerdo. Para valores pequenos de são aproximadamente iguais. Como estamos assumir que é pequeno, podemos, aproximadamente, exprimir a diferença das componentes verticais por

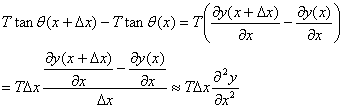
Como estamos a ignorar o movimento do segmento na direção horizontal, a diferença encontrada acima exprime a força que está a ser exercida sobre o segmento. Contudo, essa força pode ser calculada de outra forma, recorrendo à lei de Newton (F = ma). Assim, como a aceleração é dada por , a força exercida no segmento considerado é então .

Decorre então que

Se a densidade linear da corda for dada por , então a massa do segmento é , donde .

Resulta então que, para valores pequenos de , o movimento da corda satisfaz de forma bastante aproximada a equação , que escrita de outra forma corresponde à conhecida equação de onda , com , a qual foi obtida por Jean le Rond d’Alembert em 1747.

O desafio natural que surge de seguida é tentar descobrir uma solução geral da equação encontrada acima. A ideia (inspirada em d’Alembert) é começar por fatorizar o operador diferencial:

Se considerarmos a mudança de variáveis , aplicando a regra da cadeia , obtemos que .

Se diferenciarmos novamente a expressão acima em ordem a t, vem que

.

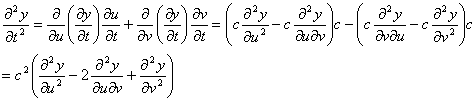De forma análoga se obtém que .

Se aplicarmos estes resultados à equação da onda, resulta que 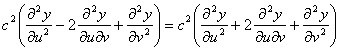, pelo que se conclui que

Procuremos agora a solução geral da equação acima. Como , resulta então que é uma função que não depende da variável u, pelo que podemos encará-la apenas como uma função de v, ou seja, .

Sendo assim, , em que é uma primitiva de e pode ser encarada como uma constante relativamente a v, resultante da integração de .

Substituindo novamente as variáveis, obtemos , e y pode assim ser interpretado como a soma de duas ondas f e g, em que f se propaga para a direita e g se propaga para a esquerda.

Como o extremos da corda mantém-se sempre imóvel, resulta então que , para todo o t, e portanto, , para qualquer . Então .

Como o outro extremo da corda permanece também sempre imóvel, resulta que , para todo o t, e portanto, , para qualquer .

Estamos, portanto, em condições de sintetizar os resultados obtidos por intermédio do seguinte teorema:

Embora a equação da onda faça sentido para qualquer função com derivadas parciais de segunda ordem, as soluções que nos interessam são aquelas em que f é contínua (o deslocamento de um acorda não pode ser expresso por uma função descontínua). Sendo f contínua e periódica, então pode ser expandida numa série de Fourier, pelo que y(x,t) também pode ser expandida numa série de Fourier. Conseqüentemente, o movimento y(a,t) (a fixo) de uma partícula da corda também pode ser expresso numa série de Fourier, como foi referido antes. A expansão de f vai refletir a presença dos movimentos harmônicos da corda:

,

em que cada harmônico n está associado à parcela n deste desenvolvimento (note-se, por exemplo, que se impedirmos a corda de vibrar livremente, então C₁= 0). A equação geral da vibração da corda é dada por

,

que pode ser escrita na forma , fazendo uso de uma identidade trigonométrica.

Cada harmônico n tem as seguintes características:

A freqüência, sendo uma noção temporal, é dada por = . Esta fórmula, que foi descoberta por Marin Marsenne, revela que a freqüência duma corda que vibra é inversamente proporcional ao seu comprimento e à raiz quadrada da sua densidade linear, sendo proporcional à raiz quadrada da sua tensão.

A amplitude máxima de cada ponto do harmônico é dada por , pelo que a amplitude de cada harmônico n pode ser caracterizada pelo seu valor máximo , que caracteriza a intensidade com que o harmônico está presente num som. Geralmente, o harmônico que tem maior intensidade é o harmônico de menor índice, pois é o que atinge maior amplitude. À freqüência desse harmônico dá-se o nome de freqüência fundamental, pois é a freqüência que mais se destaca no som a que pertence.

---

Notas:

[1] Para a Acústica, um harmónico é uma frequência pura, que pode ser descrito por uma sinusoidal, com determinada frequência e amplitude. Os sons são constituídos por vários harmónicos, não existindo na realidade sons puros, constituídos apenas por um harmónico.

---

Anexo

Índice da Seção Atual